Cách tính phần trăm đơn giản dễ hiểu cho mọi người
Tỷ lệ phần trăm, được ký hiệu là “%”, là một cách biểu diễn một phần nào đó của một tổng số dưới dạng một con số nhỏ hơn 100 lần. Nó được sử dụng phổ biến trong nhiều lĩnh vực khác nhau để so sánh, đánh giá và thể hiện mức độ tương quan giữa các đại lượng.
Hiểu rõ cách tính phần trăm là điều cần thiết cho mọi người trong cuộc sống hàng ngày. Nó giúp ta giải quyết các vấn đề liên quan đến tài chính, học tập, kinh doanh, và nhiều lĩnh vực khác. Bài viết này sẽ hướng dẫn bạn cách tính phần trăm một cách đơn giản và chính xác.
Tỷ lệ phần trăm (%) là gì?
Tỷ lệ phần trăm (%) là một cách biểu diễn một phần nào đó của một tổng thể bằng cách chia nó cho tổng thể đó và nhân với 100. Nói cách khác, tỷ lệ phần trăm cho ta biết phần trăm của một số so với một số khác, hoặc phần trăm của một đại lượng so với tổng đại lượng.
Ví dụ
- 50% nghĩa là 50/100, tức là 50 phần trong tổng số 100 phần.
- 20% giảm giá nghĩa là giá sau giảm đi 20/100 giá gốc.
- 80% dân số có độ tuổi từ 18 đến 65 nghĩa là 80/100 tổng dân số nằm trong độ tuổi này.

Ý nghĩa của tỷ lệ phần trăm
Thể hiện mối quan hệ giữa các đại lượng
Tỷ lệ phần trăm giúp ta dễ dàng so sánh hai hoặc nhiều đại lượng có đơn vị đo lường khác nhau. Ví dụ, ta có thể so sánh điểm thi môn Toán của học sinh A (80%) với điểm thi môn Văn của học sinh B (90%) để đánh giá mức độ học tập của hai học sinh này.
Đánh giá mức độ hoàn thành
Tỷ lệ phần trăm thường được sử dụng để đánh giá mức độ hoàn thành một công việc, một dự án, hoặc một mục tiêu nào đó. Ví dụ, ta có thể nói rằng một dự án đã hoàn thành 75% để thể hiện tiến độ thực hiện của dự án đó.
So sánh dữ liệu
Tỷ lệ phần trăm giúp ta dễ dàng so sánh dữ liệu thu thập được từ các nguồn khác nhau. Ví dụ, ta có thể so sánh tỷ lệ thất nghiệp của hai quốc gia để đánh giá tình hình kinh tế của mỗi quốc gia.
Đưa ra quyết định
Tỷ lệ phần trăm thường được sử dụng làm cơ sở để đưa ra các quyết định quan trọng trong kinh doanh, chính trị, và nhiều lĩnh vực khác. Ví dụ, một công ty có thể quyết định tăng giá sản phẩm của mình lên 10% dựa trên tỷ lệ lạm phát.

Công thức tính phần trăm cơ bản
Tính phần trăm của một số
Công thức
Phần trăm = (Số cần tính / Số gốc) x 100%
Ví dụ
Tính 20% của 100
Phần trăm = (20 / 100) x 100% = 20%
Ứng dụng
- Tính tỷ lệ lợi nhuận/lỗ trong kinh doanh.
- Tính điểm thi của học sinh.
- Tính tỷ lệ dân số theo độ tuổi.

Tìm số khi biết phần trăm
Công thức
Số cần tìm = (Phần trăm x Số gốc) / 100%
Ví dụ
Tìm số x khi biết 20% của x là 20
x = (20 x 100%) / 20% = 100
Ứng dụng
- Tìm giá gốc khi biết giá khuyến mãi và tỷ lệ giảm giá.
- Tìm số điểm cần đạt để đạt được một tỷ lệ điểm nhất định.
- Tìm số lượng sản phẩm cần bán để đạt được doanh thu mục tiêu.

Tính tỷ số phần trăm giữa hai số
Công thức
Tỷ số phần trăm = (Số thứ nhất / Số thứ hai) x 100%
Ví dụ
Tính tỷ số phần trăm giữa 20 và 50
Tỷ số phần trăm = (20 / 50) x 100% = 40%
Ứng dụng
- So sánh hai số liệu khác nhau về đơn vị.
- Đánh giá mức độ tăng/giảm của một đại lượng so với đại lượng khác.
Tăng/giảm một số theo tỷ lệ phần trăm
Tăng
Số mới = Số cũ x (1 + Tỷ số phần trăm tăng / 100%)
Giảm
Số mới = Số cũ x (1 – Tỷ số phần trăm giảm / 100%)
Ví dụ
Tăng 10% giá bán của một sản phẩm có giá 100.000 đồng:
Số mới = 100.000 x (1 + 10% / 100%) = 110.000 đồng
Ứng dụng
- Tính giá mới sau khi tăng/giảm thuế, VAT.
- Tính lãi suất cho khoản vay/gửi tiết kiệm.
Tính lãi suất kép
Công thức
Số tiền sau n kỳ = Số tiền gốc x (1 + Lãi suất / 100)^n
Ví dụ
Gửi tiết kiệm 1 triệu đồng với lãi suất 6%/năm sau 5 năm:
Số tiền sau 5 kỳ = 1.000.000 x (1 + 6% / 100)^5 = 1.338.225 đồng
Ứng dụng
- Tính toán lợi nhuận đầu tư sinh lời theo thời gian.
- Lập kế hoạch tiết kiệm để đạt được mục tiêu tài chính.
Ứng dụng tính phần trăm trong thực tế
Tỷ lệ phần trăm (%) là một công cụ hữu ích được sử dụng rộng rãi trong nhiều lĩnh vực để so sánh, đánh giá và thể hiện mức độ tương quan giữa các đại lượng. Dưới đây là một số ứng dụng phổ biến của tính phần trăm cùng với cách tính và ví dụ cụ thể
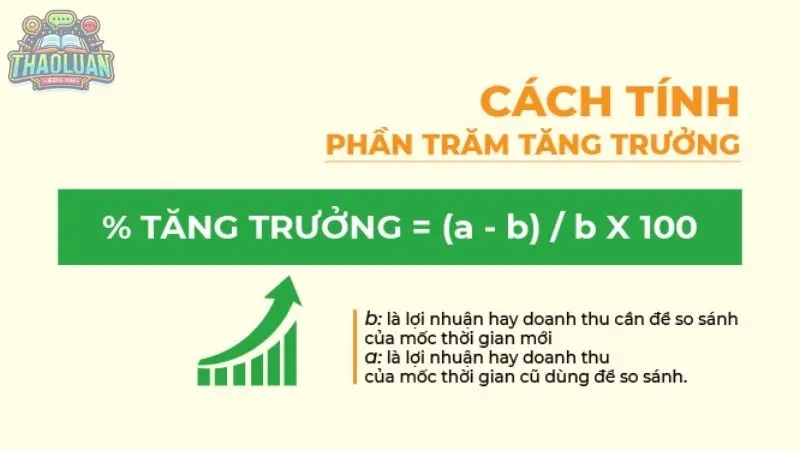
Tính phần trăm tăng trưởng
Công thức
Phần trăm tăng trưởng = ((Giá trị mới – Giá trị cũ) / Giá trị cũ) x 100%
Ví dụ: Giả sử giá một chiếc điện thoại năm ngoái là 10 triệu đồng, năm nay giảm còn 8 triệu đồng. Vậy tỷ lệ phần trăm giảm giá là: * Phần trăm giảm giá = ((8 – 10) / 10) x 100% = -20%
Lưu ý: Giá trị âm (-) thể hiện sự giảm giá.
Tính phần trăm của một tổng
Công thức
Phần trăm = (Số cần tính / Tổng số) x 100%
Ví dụ * Trong lớp học có 30 học sinh, 24 học sinh đạt điểm cao. Vậy tỷ lệ học sinh đạt điểm cao là: * Phần trăm = (24 / 30) x 100% = 80%
Tính phần trăm hoàn thành công việc
Công thức
Phần trăm hoàn thành = (Công việc đã hoàn thành / Tổng khối lượng công việc) x 100%
Ví dụ: Một dự án được chia thành 10 phần, nhóm A đã hoàn thành 7 phần. Vậy tỷ lệ phần trăm công việc nhóm A đã hoàn thành là: * Phần trăm hoàn thành = (7 / 10) x 100% = 70%

Tính phần trăm khuyến mãi
Công thức
Phần trăm khuyến mãi = (Giá khuyến mãi / Giá gốc) x 100%
Ví dụ * Một chiếc áo có giá gốc là 500.000 đồng, đang được giảm giá 20%. Vậy giá khuyến mãi của chiếc áo là: * Giá khuyến mãi = 500.000 x (1 – 20%) = 400.000 đồng * Phần trăm khuyến mãi = (400.000 / 500.000) x 100% = 80%

Tính lãi suất gửi ngân hàng
Công thức
Lãi suất = (Số tiền lãi / Số tiền gốc) x 100%
Số tiền lãi = Số tiền gốc x Lãi suất x Kỳ hạn (năm)
Ví dụ: Gửi tiết kiệm 100 triệu đồng với lãi suất 6,5%/năm trong 5 năm. Số tiền lãi nhận được sau 5 năm là: * Số tiền lãi = 100.000.000 x 6,5% x 5 = 32.500.000 đồng * Lãi suất = (32.500.000 / 100.000.000) x 100% = 32,5%
Tính lãi suất vay ngân hàng
Công thức
Lãi suất = (Số tiền lãi / Số tiền vay) x 100%
Số tiền lãi = Số tiền vay x Lãi suất x Kỳ hạn (năm)
Ví dụ * Vay ngân hàng 500 triệu đồng với lãi suất 8%/năm trong 2 năm. Số tiền lãi cần trả sau 2 năm là: * Số tiền lãi = 500.000.000 x 8% x 2 = 80.000.000 đồng * Lãi suất = (80.000.000 / 500.000.000) x 100% = 16%

Tóm lại, tính phần trăm là một kỹ năng quan trọng và hữu ích cho mọi người. Việc nắm vững các công thức và cách áp dụng tính phần trăm sẽ giúp bạn giải quyết nhiều vấn đề trong cuộc sống một cách hiệu quả. Hãy luyện tập thường xuyên để nâng cao khả năng tính toán của bạn và áp dụng nó vào thực tế một cách linh hoạt.
Ngoài ra, bạn có thể tham khảo thêm các tài liệu hướng dẫn và bài tập về tính phần trăm trên mạng hoặc sách giáo khoa để củng cố kiến thức và kỹ năng của mình.