Khám phá bí ẩn tính chất và định nghĩa hình bình hành

Trong thế giới xung quanh chúng ta, có vô số hiện tượng và đối tượng mà chúng ta có thể gặp phải hàng ngày nhưng không hẳn ai đã tìm hiểu sâu hơn về chúng. Một trong những khám phá thú vị đó là tính chất và định nghĩa của hình bình hành. Hãy cùng nhau bắt đầu hành trình khám phá sự kỳ diệu của hình bình hành và cách mà nó tồn tại và tương tác trong không gian ba chiều của chúng ta.

Khái niệm hình bình hành

Hình bình hành là một loại tứ giác có các cặp cạnh đối song song và bằng nhau. Dưới đây là khái niệm hình bình hành một cách chuẩn xác:

Khái niệm

Hình bình hành là tứ giác có các cạnh đối song song và bằng nhau.

Công thức tính diện tích

Diện tích \( S \) của hình bình hành được tính bằng tích của độ dài một cạnh đáy \( a \) và chiều cao \( h \) từ cạnh đáy đó lên cạnh đối diện:

\[ S = a \times h \]

Công thức tính chu vi

Chu vi \( P \) của hình bình hành được tính bằng tổng độ dài của bốn cạnh, hoặc bằng hai lần tổng độ dài của hai cạnh kề nhau:

\[ P = 2 \times (a + b) \]

Trong đó \( a \) và \( b \) là độ dài của hai cạnh kề nhau.

Hình bình hành có thể được coi là một trường hợp đặc biệt của hình thoi và hình chữ nhật, khi các cạnh hoặc góc có những đặc điểm tương ứng như bằng nhau hoặc vuông góc.

Ví dụ minh họa

Nếu hình bình hành có độ dài cạnh đáy \( a = 5 \) cm, chiều cao \( h = 3 \) cm, và cạnh kề \( b = 4 \) cm, thì diện tích và chu vi của nó là:

\[ S = 5 \times 3 = 15 \, \text{cm}^2 \]

\[ P = 2 \times (5 + 4) = 18 \, \text{cm} \]

Các dấu hiệu nhận biết hình bình hành

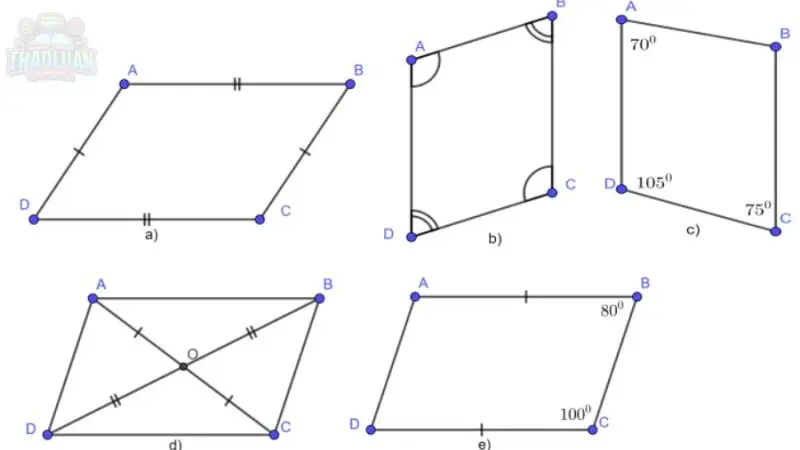
Dưới đây là các dấu hiệu nhận biết hình bình hành một cách đầy đủ và chi tiết

Dấu hiệu về cạnh

Hai cặp cạnh đối song song: Nếu một tứ giác có hai cặp cạnh đối song song, tứ giác đó là hình bình hành.

Ví dụ: Nếu AB // CD và AD // BC, thì ABCD là hình bình hành.

Hai cặp cạnh đối bằng nhau: Nếu một tứ giác có hai cặp cạnh đối bằng nhau, tứ giác đó là hình bình hành.

Ví dụ: Nếu AB = CD và AD = BC, thì ABCD là hình bình hành.

Dấu hiệu về góc

Hai cặp góc đối bằng nhau: Nếu một tứ giác có hai cặp góc đối bằng nhau, tứ giác đó là hình bình hành.

Ví dụ: Nếu góc A = góc C và góc B = góc D, thì ABCD là hình bình hành.

Hai góc kề bù nhau: Nếu một tứ giác có hai góc kề nhau bù nhau (tổng bằng 180 độ), và điều này xảy ra cho tất cả các cặp góc kề, thì tứ giác đó là hình bình hành.

Ví dụ: Nếu góc A + góc B = 180 độ và góc C + góc D = 180 độ, thì ABCD là hình bình hành.

Dấu hiệu về đường chéo

Hai đường chéo cắt nhau tại trung điểm của mỗi đường: Nếu một tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường, tứ giác đó là hình bình hành.

Ví dụ: Nếu đường chéo AC và BD cắt nhau tại O, và O là trung điểm của cả AC và BD, thì ABCD là hình bình hành.

Các dấu hiệu tổng hợp

Một cặp cạnh đối vừa song song vừa bằng nhau: Nếu một tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau, tứ giác đó là hình bình hành.

Ví dụ: Nếu AB // CD và AB = CD, thì ABCD là hình bình hành.

Tóm tắt

• Hai cặp cạnh đối song song.
• Hai cặp cạnh đối bằng nhau.
• Hai cặp góc đối bằng nhau.
• Hai góc kề bù nhau (tổng bằng 180 độ).
• Hai đường chéo cắt nhau tại trung điểm của mỗi đường.
• Một cặp cạnh đối vừa song song vừa bằng nhau.

Những dấu hiệu trên giúp nhận biết và xác định hình bình hành một cách chính xác, áp dụng vào việc giải các bài toán hình học cũng như trong thực tế.

Ví dụ về hình bình hành

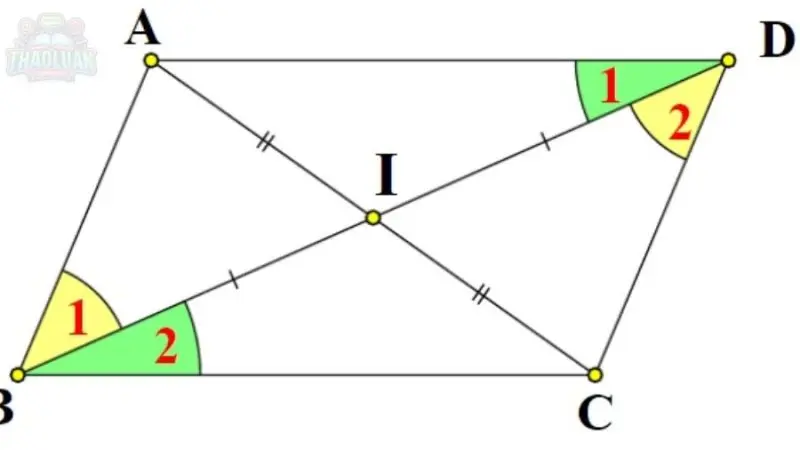
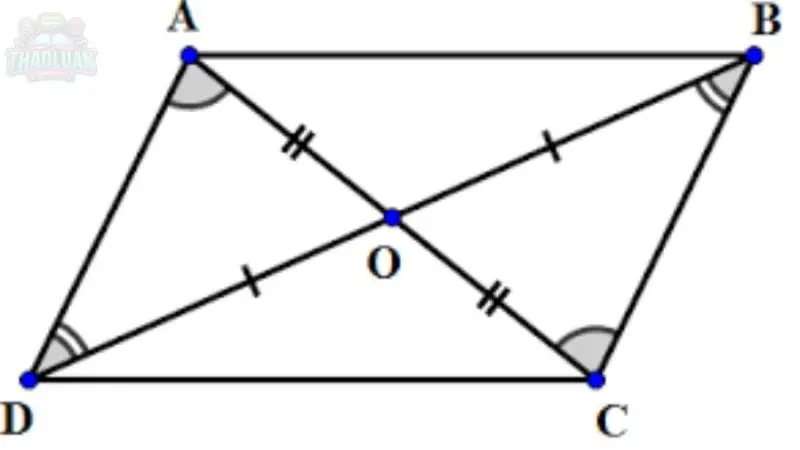
Dưới đây là một ví dụ cụ thể về hình bình hành, kèm theo các yếu tố giúp nhận biết hình bình hành này.

Ví dụ về hình bình hành

Giả sử ta có tứ giác ABCD với các đặc điểm sau

Cạnh:

Độ dài cạnh AB = 6 cm

Độ dài cạnh BC = 4 cm

Độ dài cạnh CD = 6 cm

Độ dài cạnh DA = 4 cm

Góc:

Góc A = 110 độ

Góc B = 70 độ

Góc C = 110 độ

Góc D = 70 độ

Đường chéo

Đường chéo AC và BD cắt nhau tại điểm O

O là trung điểm của cả AC và BD

Xác minh tứ giác ABCD là hình bình hành

Hai cặp cạnh đối song song và bằng nhau

AB = CD = 6 cm

AD = BC = 4 cm

Hai cặp góc đối bằng nhau

Góc A = Góc C = 110 độ

Góc B = Góc D = 70 độ

Tổng các góc kề nhau bằng 180 độ

Góc A + Góc B = 110 độ + 70 độ = 180 độ

Góc B + Góc C = 70 độ + 110 độ = 180 độ

Hai đường chéo cắt nhau tại trung điểm của mỗi đường

Đường chéo AC và BD cắt nhau tại O, và O là trung điểm của cả AC và BD

Dựa trên các yếu tố trên, ta có thể xác định tứ giác ABCD là một hình bình hành.

Công thức tính diện tích và chu vi:

Diện tích (S)

Giả sử chiều cao từ cạnh đáy AB xuống cạnh CD là 3 cm

Diện tích \( S = a \times h = 6 \, \text{cm} \times 3 \, \text{cm} = 18 \, \text{cm}^2 \)

Chu vi (P):

Chu vi \( P = 2 \times (a + b) = 2 \times (6 \, \text{cm} + 4 \, \text{cm}) = 20 \, \text{cm} \)

Ứng dụng hình bình hành

Hình bình hành là một hình học cơ bản với nhiều ứng dụng trong đời sống thực tế và các lĩnh vực khoa học. Dưới đây là một số ứng dụng chính của hình bình hành:

Ứng dụng trong kiến trúc và xây dựng

Thiết kế kết cấu: Hình bình hành được sử dụng trong thiết kế các khung cửa, cửa sổ, mái nhà và cầu. Các cạnh song song và bằng nhau của hình bình hành giúp phân bổ lực đều, tăng độ bền vững cho kết cấu.

Lát gạch và ốp tường: Các viên gạch hoặc tấm lát hình bình hành thường được sử dụng để tạo ra các mẫu trang trí độc đáo trên sàn và tường.

Ứng dụng trong kỹ thuật và cơ học

Cơ cấu chuyển động: Trong các cơ cấu cơ khí, hình bình hành giúp chuyển động tuyến tính sang chuyển động quay và ngược lại. Ví dụ, các cơ cấu đòn bẩy và cánh tay robot thường sử dụng hình bình hành để đảm bảo chuyển động chính xác.

Thiết kế đường chéo: Đường chéo trong hình bình hành thường được sử dụng trong việc tính toán và thiết kế các kết cấu chịu lực, chẳng hạn như dầm và giàn giáo.

Ứng dụng trong đồ họa và thiết kế

Đồ họa máy tính: Hình bình hành được sử dụng trong các thuật toán đồ họa máy tính để tạo ra các hình ảnh 3D từ các tọa độ 2D.

Thiết kế thời trang: Các mẫu vải hình bình hành thường xuất hiện trong thiết kế thời trang để tạo ra các hoa văn độc đáo và bắt mắt.

Ứng dụng trong toán học và giáo dục

Hình học Euclid: Hình bình hành là một phần quan trọng trong chương trình giảng dạy hình học, giúp học sinh hiểu về các tính chất của tứ giác và các định lý hình học cơ bản.

Bài toán diện tích và chu vi: Hình bình hành giúp học sinh thực hành các bài toán tính diện tích và chu vi, từ đó củng cố kiến thức về công thức và phương pháp tính toán.

Ứng dụng trong vật lý

Lực và mô-men lực: Hình bình hành được sử dụng để minh họa các nguyên lý về lực và mô-men lực trong vật lý, chẳng hạn như quy tắc hình bình hành để cộng hai vectơ lực.

Quang học: Các gương và lăng kính hình bình hành được sử dụng để khúc xạ và phản xạ ánh sáng trong các thiết bị quang học.

Ứng dụng trong đời sống hàng ngày

Nghệ thuật và trang trí: Hình bình hành xuất hiện trong nhiều tác phẩm nghệ thuật và thiết kế nội thất, tạo ra các mẫu trang trí thú vị và hài hòa.

Gương và kính mắt: Các gương và tròng kính hình bình hành được thiết kế để tối ưu hóa góc nhìn và phản xạ ánh sáng.

Ví dụ minh họa

Cầu thang: Bậc thang thường được thiết kế dưới dạng hình bình hành để đảm bảo độ nghiêng và chiều cao bước phù hợp.

Đồng hồ: Một số mặt đồng hồ có hình dạng hình bình hành để tạo sự khác biệt và thu hút.

Hình bình hành không chỉ là một hình học cơ bản trong toán học mà còn có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau của cuộc sống và công nghệ. Việc hiểu rõ và vận dụng các tính chất của hình bình hành giúp chúng ta giải quyết nhiều bài toán thực tiễn một cách hiệu quả.

Hy vọng rằng qua bài viết này, bạn đã có được những kiến thức hữu ích và hiểu rõ hơn về tính chất cũng như định nghĩa của hình bình hành. Hình bình hành không chỉ là một khái niệm cơ bản trong hình học mà còn chứa đựng nhiều điều thú vị và ứng dụng thực tiễn trong cuộc sống.

Từ việc xác định các tính chất đặc trưng như các cạnh đối song song và bằng nhau, góc đối bằng nhau, đến việc áp dụng vào giải các bài toán thực tế, hình bình hành đóng vai trò quan trọng trong cả lý thuyết và thực hành.