Tổng hợp các kiến thức định nghĩa hình chữ nhật

Hình chữ nhật là một trong những hình học cơ bản và phổ biến nhất mà chúng ta gặp phải trong cả cuộc ống hàng ngày lẫn trong các bài toán hình học. Từ những cuốn sách giáo khoa cho đến các công trình kiến trúc phức tạp, hình chữ nhật đóng vai trò quan trọng trong việc định hình không gian và cấu trúc. Hiểu rõ về hình chữ nhật không chỉ giúp bạn giải quyết những vấn đề toán học một cách hiệu quả mà còn mở rộng khả năng áp dụng kiến thức này vào thực tiễn.

Trong bài viết này, chúng ta sẽ tổng hợp các kiến thức cơ bản và định nghĩa quan trọng về hình chữ nhật. Bạn sẽ được tìm hiểu về các tính chất, công thức, và ứng dụng thực tiễn của hình học này. Hãy cùng khám phá và củng cố hiểu biết của bạn về hình chữ nhật, một trong những nền tảng của hình học phẳng.

Định nghĩa hình chữ nhật

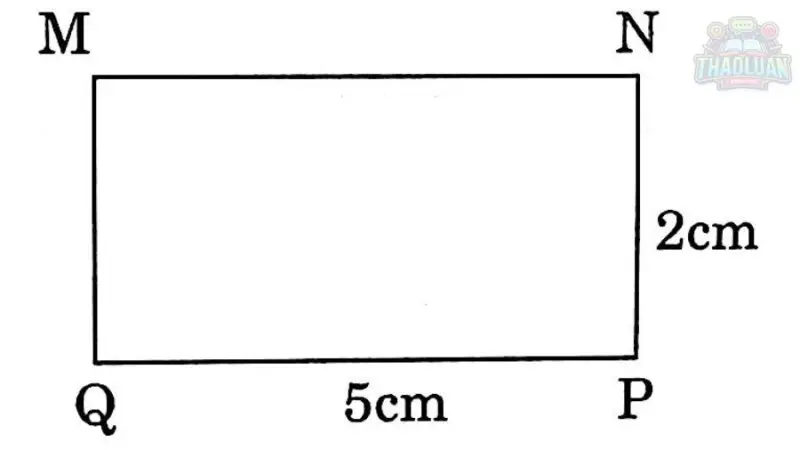
“Hình chữ nhật là một hình học phẳng có bốn góc vuông và bốn cạnh. Các đặc điểm chính của hình chữ nhật bao gồm hai cặp cạnh song song có độ dài bằng nhau và hai cặp góc vuông. Với hai cặp cạnh song song đối diện có độ dài bằng nhau, hình chữ nhật có thể được định nghĩa bằng hai kích thước: chiều dài và chiều rộng. Diện tích của hình chữ nhật được tính bằng cách nhân chiều dài và chiều rộng với nhau. Đây là một trong những hình dạng cơ bản nhất và phổ biến nhất trong toán học và hình học, và có nhiều ứng dụng trong thực tế từ kiến trúc đến thiết kế công nghiệp.”

Các yếu tố của hình chữ nhật

Cạnh:

Hình chữ nhật có bốn cạnh.

Hai cặp cạnh song song có độ dài bằng nhau.

Góc:

Hình chữ nhật có bốn góc vuông.

Góc giữa mỗi cặp cạnh là 90 độ.

Chiều dài và chiều rộng:

Hai kích thước cơ bản của hình chữ nhật là chiều dài và chiều rộng.

Chiều dài là đoạn thẳng nối hai đỉnh đối diện của hình chữ nhật, song song với cạnh dài hơn.

Chiều rộng là đoạn thẳng nối hai đỉnh đối diện của hình chữ nhật, song song với cạnh ngắn hơn.

Đường chéo:

Đường chéo của hình chữ nhật là đoạn thẳng nối hai đỉnh không kề nhau của hình chữ nhật.

Đường chéo cũng là đường chính đối xứng của hình chữ nhật.

Các yếu tố này cùng tạo nên bản chất và tính chất cơ bản của hình chữ nhật, giúp chúng ta hiểu rõ hơn về hình dạng và tính toán của nó.

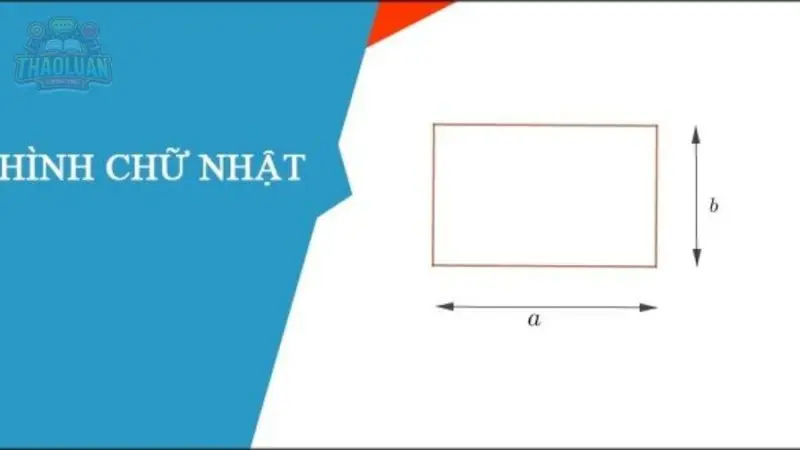
Diện tích và chu vi hình chữ nhật

Để tính diện tích và chu vi của hình chữ nhật, chúng ta cần biết hài kích thước cơ bản của nó là chiều dài và chiều rộng. Sau đây là cách tính diện tích và chu vi của hình chữ nhật:

Diện tích (S):

Diện tích của hình chữ nhật được tính bằng cách nhân chiều dài và chiều rộng với nhau.

Công thức: \( S = \text{Chiều dài} \times \text{Chiều rộng} \).

Chu vi (P):

Chu vi của hình chữ nhật được tính bằng tổng độ dài của tất cả các cạnh.

Công thức: \( P = 2 \times (\text{Chiều dài} + \text{Chiều rộng}) \).

Ví dụ: Giả sử chiều dài của hình chữ nhật là 5 đơn vị và chiều rộng là 3 đơn vị.

Diện tích:

\( S = 5 \times 3 = 15 \) đơn vị vuông.

Chu vi:

\( P = 2 \times (5 + 3) = 2 \times 8 = 16 \) đơn vị.

Như vậy, diện tích của hình chữ nhật là 15 đơn vị vuông và chu vi là 16 đơn vị.

Ví dụ về hình chữ nhật trong thực tế

Ví dụ về hình chữ nhật trong thực tế có thể giúp làm rõ và minh họa cách mà khái niệm này được áp dụng trong cuộc sống hàng ngày. Dưới đây là một ví dụ về hình chữ nhật trong thực tế:

Ví dụ: Sử dụng hình chữ nhật trong thiết kế nội thất

Trong thiết kế nội thất, hình chữ nhật thường được sử dụng để tạo ra các khu vực phân chia và bố trí không gian một cách hợp lý và hài hòa. Ví dụ, một phòng khách có thể được bố trí với một bức tường chính là một hình chữ nhật lớn, giúp chia phòng thành các khu vực như khu vực tiếp khách, khu vực giải trí, và khu vực ăn uống.

Tính thẩm mỹ: Hình chữ nhật có thể tạo ra sự cân đối và sự giao thoa hài hòa giữa các yếu tố khác nhau trong không gian.

Tính chức năng: Bằng cách sử dụng hình chữ nhật, không gian có thể được tối ưu hóa để phục vụ các mục đích cụ thể như giải trí, nghỉ ngơi, làm việc, hoặc ăn uống.

Tính thông tin: Việc sử dụng hình chữ nhật trong thiết kế nội thất cũng có thể được tận dụng trong việc tạo điểm nhấn hoặc tạo ra các khu vực chức năng riêng biệt.

Bài tập liên quan đến hình chữ nhật

Dưới đây là một số bài tập liên quan đến hình chữ nhật để bạn luyện tập.

Bài tập 1: Tính diện tích và chu vi hình chữ nhật

Cho hình chữ nhật có chiều dài là 8 cm và chiều rộng là 5 cm. Tính diện tích và chu vi của hình chữ nhật này.

Một hình chữ nhật có chiều dài gấp đôi chiều rộng và chu vi bằng 24 cm. Tìm chiều dài và chiều rộng của hình chữ nhật này.

Bài tập 2: Tìm chiều dài hoặc chiều rộng

Cho biết diện tích của một hình chữ nhật là 56 cm² và chiều rộng là 7 cm. Tìm chiều dài của hình chữ nhật.

Một hình chữ nhật có diện tích là 72 cm² và chiều dài gấp ba lần chiều rộng. Tìm chiều dài và chiều rộng của hình chữ nhật.

Bài tập 3: Ứng dụng thực tế

Một miếng đất hình chữ nhật có chiều dài 20 m và chiều rộng 15 m. Người ta muốn rào xung quanh miếng đất này bằng dây thép gai. Tính chiều dài dây thép gai cần dùng.

Một tấm bảng hình chữ nhật có diện tích 1,5 m² và chiều dài là 1,2 m. Hãy tính chiều rộng của tấm bảng.

Bài tập 4: Hình chữ nhật đặc biệt

Hãy tính diện tích và chu vi của một hình vuông có cạnh là 6 cm. Sau đó, so sánh với diện tích và chu vi của một hình chữ nhật có chiều dài và chiều rộng bằng cạnh của hình vuông đó.

Đáp án

Bài tập 1:

   – Diện tích: \( A = D \times R = 8 \, \text{cm} \times 5 \, \text{cm} = 40 \, \text{cm}^2 \)

   – Chu vi: \( P = 2 \times (D + R) = 2 \times (8 \, \text{cm} + 5 \, \text{cm}) = 26 \, \text{cm} \)

   – Giả sử chiều dài là \( l \), chiều rộng là \( w \). Ta có \( l = 2w \) và chu vi: \( P = 2 \times (l + w) = 24 \)

   – Thay \( l = 2w \) vào: \( 2 \times (2w + w) = 24 \) -> \( 6w = 24 \) -> \( w = 4 \) cm

   – \( l = 2w = 8 \) cm

Bài tập 2:

   – Diện tích \( A = l \times w = 56 \)

   – Chiều rộng \( w = 7 \) cm -> \( l = \frac{A}{w} = \frac{56}{7} = 8 \) cm 

   – Giả sử chiều rộng là \( w \), chiều dài là \( l = 3w \). Diện tích: \( A = l \times w = 72 \)

   – Thay \( l = 3w \) vào: \( 3w \times w = 72 \) -> \( 3w^2 = 72 \) -> \( w^2 = 24 \) -> \( w = \sqrt{24} = 2\sqrt{6} \)

   – \( l = 3w = 6\sqrt{6} \)

Bài tập 3:

   – Chu vi: \( P = 2 \times (D + R) = 2 \times (20 \, \text{m} + 15 \, \text{m}) = 70 \, \text{m} \)

   – Diện tích \( A = l \times w = 1,5 \, \text{m}^2 \)

   – Chiều dài \( l = 1,2 \) m -> \( w = \frac{A}{l} = \frac{1,5}{1,2} = 1,25 \) m

Bài tập 4:

   – Hình vuông có cạnh \( a = 6 \) cm: Diện tích \( A = a^2 = 36 \, \text{cm}^2 \); Chu vi \( P = 4a = 24 \, \text{cm} \)

   – Hình chữ nhật có chiều dài và chiều rộng đều là 6 cm (như hình vuông): Diện tích \( A = 6 \times 6 = 36 \, \text{cm}^2 \); Chu vi \( P = 2 \times (6 + 6) = 24 \, \text{cm} \)

Trong bài viết này, chúng ta đã tìm hiểu về hình chữ nhật từ các khái niệm cơ bản như định nghĩa, các yếu tố và tính toán diện tích, chu vi, đến cách áp dụng của nó trong thực tế. Bằng cách cung cấp ví dụ cụ thể và minh họa, chúng ta đã thấy được sự linh hoạt và đa dạng của hình chữ nhật trong các lĩnh vực khác nhau như thiết kế nội thất.

Hy vọng rằng thông qua bài viết này, bạn đã có cái nhìn rõ ràng và toàn diện hơn về hình chữ nhật, cũng như hiểu biết sâu sắc hơn về cách áp dụng nó trong thực tế. Nếu có bất kỳ thắc mắc hoặc góp ý nào, xin đừng ngần ngại để lại cho chúng tôi biết.