Định nghĩa hình thang là gì? Dấu hiệu nhận biết hình thang

Hình thang là một trong những hình học phổ biến và thú vị, với nhiều tính chất độc đáo và ứng dụng đa dạng trong cuộc sống hàng ngày cũng như trong lĩnh vực toán học và kỹ thuật. Trên cơ sở các đặc điểm và tính chất riêng biệt, hình thang không chỉ là một hình dạng đẹp mắt mà còn là một công cụ mạnh mẽ để giải quyết các vấn đề phức tạp. 

Trong phần tiếp theo, chúng ta sẽ khám phá hình thang từ các khái niệm cơ bản đến các ứng dụng thực tiễn, giúp bạn hiểu rõ hơn về hình thang và khám phá tiềm năng của nó. Hãy cùng chúng tôi đắm chìm vào thế giới hình học và khám phá hình thang, một trong những hình dạng đặc biệt và đa chiều nhất trong toán học.

Khái niệm hình thang 

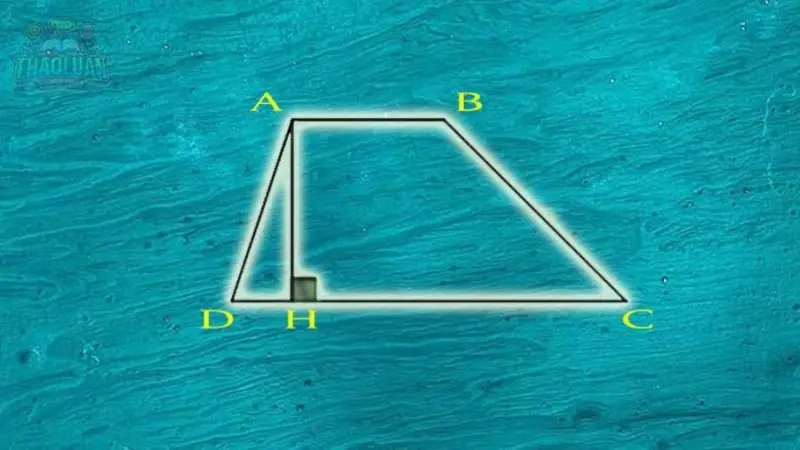
Hình thang là một hình học phẳng có bốn cạnh, trong đó hai cạnh đối diện (gọi là các cạnh đáy) là song song và có độ dài khác nhau, và hai cạnh còn lại (gọi là các cạnh bên) cũng có độ dài khác nhau nhưng không song song. Hình thang có hai cặp góc ở đỉnh đối diện nhau bằng nhau, và tổng độ dài của hai cạnh đáy là đủ lớn để hai đường thẳng này không giao nhau bên ngoài hình thang.

Các đặc điểm chính của hình thang bao gồm:

Cạnh đáy: Hai cạnh đáy là hai cạnh đối diện của hình thang, song song với nhau nhưng có độ dài khác nhau.

Cạnh bên: Hai cạnh bên của hình thang là hai cạnh còn lại, chúng không song song với nhau và có độ dài khác nhau.

Góc đỉnh: Hai cặp góc ở đỉnh đối diện nhau trong hình thang bằng nhau.

Chiều cao: Chiều cao của hình thang là đoạn thẳng vuông góc với hai cạnh đáy và nối chúng lại với nhau.

Hình thang thường được sử dụng trong nhiều lĩnh vực, từ hình học cơ bản đến các bài toán tính toán phức tạp và trong thiết kế đồ họa. Đặc biệt, trong hình học, hình thang là một trường hợp đặc biệt của hình bình hành với một trong các góc bị uốn cong.

Phân loại hình thang

Phân loại hình thang là một cách để tổ chức và phân biệt các loại hình thang dựa trên các đặc điểm cụ thể của chúng. Việc này không chỉ giúp cho người đọc hiểu rõ hơn về sự đa dạng của hình thang mà còn giúp tối ưu hóa cho công cụ tìm kiếm. 

Theo các cạnh đáy

Hình thang cân: Hai cạnh đáy của hình thang cân có độ dài bằng nhau.

Hình thang không cân: Hai cạnh đáy của hình thang không cân có độ dài không bằng nhau.

Theo các góc

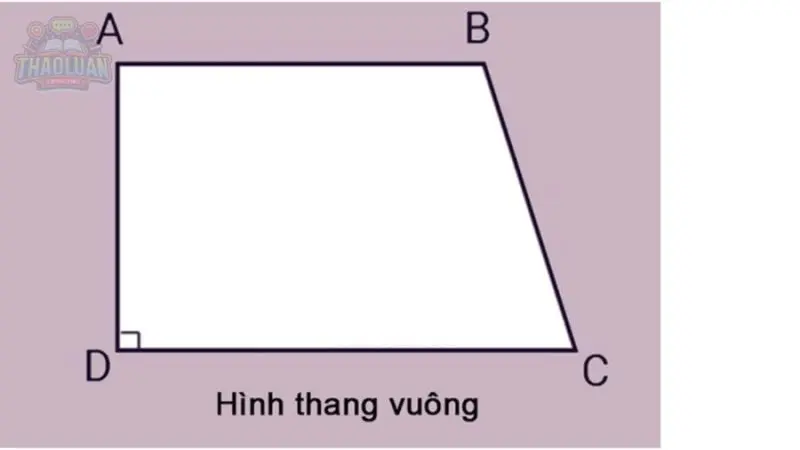
Hình thang vuông: Có một góc trong hình thang là góc vuông.

Hình thang nhọn: Tất cả các góc trong hình thang đều nhọn.

Hình thang tù: Tất cả các góc trong hình thang đều tù.

Theo tính chất khác

Hình thang đều: Cả bốn cạnh và cả bốn góc trong hình thang đều bằng nhau.

Hình thang chia đôi: Đường chéo của hình thang chia nó thành hai tam giác có diện tích bằng nhau.

Các yếu tố của hình thang

Các yếu tố chính của hình thang bao gồm:

Cạnh đáy:

Hình thang có hai cạnh đáy, đó là hai cạnh đối diện và song song của hình thang.

Cạnh bên:

Hình thang cũng có hai cạnh bên, đó là hai cạnh còn lại, không song song với nhau.

Góc:

Hình thang có bốn góc, trong đó hai góc ở đỉnh đối diện nhau bằng nhau.

Góc giữa cạnh đáy và cạnh bên được gọi là góc nội tiếp của hình thang.

Đường chéo:

Đường chéo của hình thang là đoạn thẳng nối hai đỉnh không kề nhau của hình thang.

Đường chéo chia hình thang thành hai tam giác.

Chiều cao:

Chiều cao của hình thang là đoạn thẳng vuông góc với cạnh đáy và cạnh bên, nối chúng lại với nhau.

Chiều cao là đường vuông góc với hai cạnh đáy và cắt qua đỉnh của hình thang.

Các yếu tố này định nghĩa các đặc điểm cơ bản và quan trọng của hình thang, giúp chúng ta hiểu rõ hơn về hình dạng và tính toán của nó.

Công thức tính diện tích của hình thang

\[ S = \frac{{(a + b) \times h}}{2} \]

Trong đó:

 \( S \) là diện tích của hình thang.

 \( a \) và \( b \) là độ dài của hai cạnh đáy (các cạnh song song của hình thang).

 \( h \) là chiều cao của hình thang (khoảng cách giữa hai cạnh đáy, vuông góc với chúng).

Bằng cách nhân tổng độ dài hai cạnh đáy với chiều cao và chia cho hai, chúng ta có thể tính được diện tích của hình thang.

Các tính chất của hình thang

Ngoài những tính chất cơ bản đã được đề cập, hình thang còn có một số tính chất khác đặc biệt:

Đường chéo phân giác

Đường chéo của hình thang chia góc giữa hai cạnh đáy thành hai góc bằng nhau.

Điều này có nghĩa là đường chéo là đường phân giác của góc giữa hai cạnh đáy.

Đối diện là bằng nhau

Độ dài của hai cạnh bên đối diện nhau trong hình thang là bằng nhau.

Điều này có nghĩa là cặp đường chéo của hình thang có độ dài bằng nhau.

Các góc liên tiếp bù

Các góc liên tiếp của hình thang bù nhau.

Nếu một góc là \( \alpha \), thì góc liên tiếp sẽ là \( 180^\circ – \alpha \).

Diện tích bằng tích chiều cao và khoảng cách giữa đáy:

Diện tích của hình thang cũng có thể được tính bằng tích của chiều cao và khoảng cách giữa hai cạnh đáy.

\( S = h \times d \), trong đó \( h \) là chiều cao và \( d \) là khoảng cách giữa hai cạnh đáy.

Những tính chất này cũng là những đặc điểm quan trọng của hình thang, giúp ta hiểu rõ hơn về tính chất và ứng dụng của nó trong các bài toán hình học.

Ứng dụng của hình thang

Hình thang là một hình học cơ bản với nhiều ứng dụng trong thực tế và các lĩnh vực khác nhau. Dưới đây là một số ứng dụng phổ biến của hình thang:

Kiến trúc và xây dựng: Trong kiến trúc, hình thang thường được sử dụng để thiết kế các mặt nghiêng của các tòa nhà và cấu trúc khác.

Các mái hình thang cũng là một ví dụ phổ biến của ứng dụng hình thang trong kiến trúc.

Thiết kế nội thất: Trong thiết kế nội thất, hình thang có thể được sử dụng để tạo ra các hình dạng và cấu trúc độc đáo cho các bức tường, cửa sổ, bàn, và ghế.

Địa hình và đo đạc: Trong địa hình và đo đạc, hình thang có thể được sử dụng để đo diện tích các khu vực không đều hoặc để tính toán các khoảng cách và chiều cao.

Công nghệ và kỹ thuật:Trong công nghệ và kỹ thuật, hình thang có thể được sử dụng để thiết kế các bộ phận máy móc và cấu trúc kỹ thuật phức tạp.

Toán học và giáo dục: Trong giáo dục, hình thang thường được sử dụng để giảng dạy về các khái niệm cơ bản của hình học và để giải quyết các bài toán tính toán.

Thể thao và giải trí:Trong thể thao, các sân chơi và sân thi đấu thường có hình thang, như sân bóng đá hoặc sân cỏ đánh golf.

Những ứng dụng này chỉ là một phần nhỏ của các cách mà hình thang có thể được sử dụng trong thực tế. Hình thang là một hình học đa dạng và linh hoạt, có thể được áp dụng trong nhiều lĩnh vực khác nhau với nhiều mục đích khác nhau.

Hình thang không chỉ là một hình học cơ bản mà còn là một công cụ quan trọng trong thực tế với nhiều ứng dụng đa dạng. Từ kiến trúc đến địa hình, từ công nghệ đến giáo dục, hình thang có mặt ở khắp mọi nơi, mang lại giá trị và tiện ích trong cuộc sống hàng ngày.

Hy vọng rằng qua bài viết này, bạn đã có cái nhìn tổng quan và sâu sắc hơn về hình thang, từ các khái niệm cơ bản đến các ứng dụng thực tiễn. Chúng tôi mong rằng thông qua việc tìm hiểu và áp dụng kiến thức về hình thang, bạn có thể tận dụng được tiềm năng của nó trong công việc và cuộc sống của mình.