Khám phá định nghĩa khối lập phương: Từ cơ bản đến ứng dụng
Trong hình học không gian, khối lập phương là một khái niệm cơ bản nhưng có nhiều ứng dụng quan trọng trong cuộc sống và công nghệ. Khối lập phương, hay còn gọi là hình hộp vuông, là một hình đa diện đều với sáu mặt vuông bằng nhau, tám đỉnh và mười hai cạnh bằng nhau. Với sự đơn giản và tính đối xứng cao, khối lập phương không chỉ là đối tượng nghiên cứu quan trọng trong toán học mà còn đóng vai trò thiết yếu trong nhiều lĩnh vực từ kiến trúc, kỹ thuật đến thiết kế và sản xuất.
Định nghĩa khối lập phương

Khối lập phương, còn gọi là hình hộp vuông, là một hình đa diện đều trong không gian ba chiều. Mỗi mặt của khối lập phương là một hình vuông, và tất cả các mặt đều có cùng kích thước. Một khối lập phương có các đặc điểm sau:
Sáu mặt vuông: Tất cả các mặt đều là hình vuông và bằng nhau.
Tám đỉnh: Các đỉnh là các điểm giao nhau của ba cạnh.
Mười hai cạnh: Mỗi cạnh có cùng độ dài, là nơi hai mặt tiếp giáp nhau.
Các góc đều bằng 90 độ: Mỗi góc giữa hai cạnh kề nhau đều là góc vuông.
Toán học mô tả khối lập phương với độ dài cạnh \( a \), diện tích bề mặt \( 6a^2 \), và thể tích \( a^3 \).
Khối lập phương là một hình học đơn giản nhưng có nhiều ứng dụng thực tế, từ thiết kế và xây dựng đến lập trình và đồ họa máy tính.
Tính chất của khối lập phương
Khối lập phương có nhiều tính chất đặc trưng quan trọng trong hình học không gian, bao gồm
Tính chất hình học
Sáu mặt vuông bằng nhau: Mỗi mặt của khối lập phương là một hình vuông có cùng diện tích.
Mười hai cạnh bằng nhau: Tất cả các cạnh của khối lập phương đều có cùng chiều dài.
Tám đỉnh: Khối lập phương có tám đỉnh, mỗi đỉnh là giao điểm của ba cạnh.
Góc vuông: Các góc giữa bất kỳ hai cạnh kề nhau đều là góc vuông (90 độ).
Diện tích và thể tích
Diện tích bề mặt: Tổng diện tích của sáu mặt vuông của khối lập phương. Nếu \( a \) là chiều dài cạnh của khối lập phương, thì diện tích bề mặt \( S \) được tính bằng:
\[S = 6a^2\]
Thể tích: Thể tích của khối lập phương được tính bằng chiều dài cạnh lập phương. Nếu \( a \) là chiều dài cạnh của khối lập phương, thì thể tích \( V \) được tính bằng
\[V = a^3 \]
Đối xứng
Đối xứng tâm: Khối lập phương có một điểm đối xứng tại trung tâm của nó.
Đối xứng mặt phẳng: Khối lập phương có ba mặt phẳng đối xứng chia nó thành hai phần bằng nhau.
Đối xứng trục: Khối lập phương có bốn trục đối xứng đi qua trung tâm và giữa các cặp mặt đối diện.
Tính chất góc cạnh
Góc giữa các mặt: Góc giữa bất kỳ hai mặt kề nhau của khối lập phương đều là 90 độ.
Góc giữa các cạnh không kề nhau: Góc giữa các cạnh không kề nhau, nằm trên các mặt khác nhau, có thể là 45 độ hoặc 90 độ tùy theo cách đo.
Đường chéo
Đường chéo mặt: Đường chéo của mỗi mặt vuông của khối lập phương. Độ dài đường chéo mặt \( d \) được tính bằng
\[d = a\sqrt{2}\]
Đường chéo không gian: Đường chéo đi từ một đỉnh của khối lập phương đến đỉnh đối diện trong không gian ba chiều. Độ dài đường chéo không gian \( D \) được tính bằng:
\[D = a\sqrt{3}\]
Những tính chất này làm cho khối lập phương trở thành một trong những hình học cơ bản và dễ nhận biết nhất, đồng thời có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau từ toán học, kiến trúc đến đồ họa máy tính và thiết kế công nghiệp.
Công thức tính toán khối lập phương
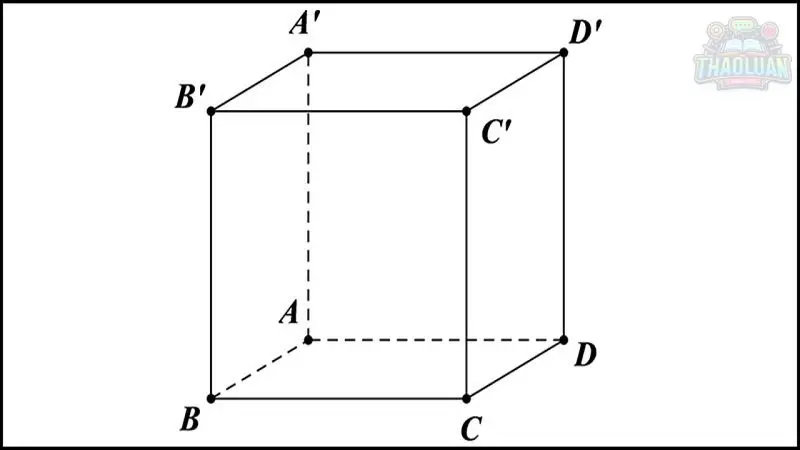
Khối lập phương có nhiều công thức tính toán liên quan đến các đặc điểm hình học cơ bản của nó. Dưới đây là các công thức quan trọng:
Chiều dài cạnh
Ký hiệu: \(a\)
Nếu biết diện tích bề mặt hoặc thể tích, bạn có thể tính chiều dài cạnh \(a\).
Diện tích mặt bên
Công thức: \(A = a^2\)
Trong đó: \(a\) là chiều dài cạnh.
Diện tích toàn phần
Công thức: \(S = 6a^2\)
Diện tích toàn phần của khối lập phương là tổng diện tích của sáu mặt vuông.
Thể tích
Công thức: \(V = a^3\)
Thể tích của khối lập phương là lập phương của chiều dài cạnh.
Đường chéo mặt
Công thức: \(d = a\sqrt{2}\)
Đây là độ dài đường chéo của mỗi mặt vuông của khối lập phương.
Đường chéo không gian
Công thức: \(D = a\sqrt{3}\)
Đây là độ dài đường chéo từ một đỉnh của khối lập phương đến đỉnh đối diện trong không gian ba chiều.
Ví dụ minh họa
Giả sử chúng ta có một khối lập phương với chiều dài cạnh \(a = 4\) cm. Chúng ta sẽ tính các đặc điểm sau
Diện tích mặt bên
\[A = a^2 = 4^2 = 16 \text{ cm}^2\]
Diện tích toàn phần
\[S = 6a^2 = 6 \times 16 = 96 \text{ cm}^2 \]
Thể Tích:
\[V = a^3 = 4^3 = 64 \text{ cm}^3 \]
Đường chéo mặt
\[d = a\sqrt{2} = 4\sqrt{2} \approx 5.66 \text{ cm}\]
Đường chéo không gian
\[D = a\sqrt{3} = 4\sqrt{3} \approx 6.93 \text{ cm}\]
Những công thức này giúp bạn tính toán các đặc điểm quan trọng của khối lập phương, từ đó ứng dụng vào nhiều lĩnh vực khác nhau như kiến trúc, thiết kế, kỹ thuật và giáo dục.
Ứng dụng của khối lập phương
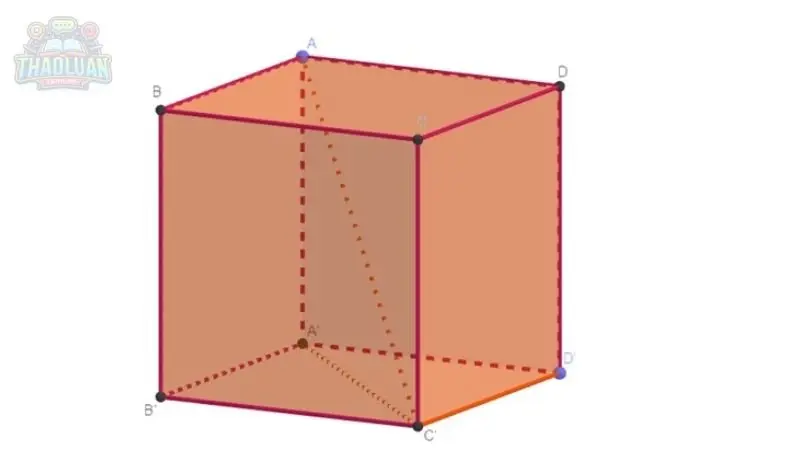
Khối lập phương có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau nhờ vào tính chất hình học đơn giản và đối xứng của nó. Dưới đây là một số ứng dụng nổi bật của khối lập phương:
Kiến trúc và xây dựng
Thiết kế tòa nhà: Nhiều công trình kiến trúc, đặc biệt là các tòa nhà và cấu trúc hiện đại, sử dụng hình dạng khối lập phương để tạo nên những không gian hiệu quả và đẹp mắt.
Kết cấu và khung sườn: Khối lập phương được dùng trong thiết kế khung sườn của các công trình xây dựng nhờ vào tính đối xứng và ổn định của nó.
Đồ họa máy tính và thiết kế 3d
Mô hình hóa đối tượng: Trong đồ họa máy tính và thiết kế 3D, khối lập phương thường được sử dụng như một khối cơ bản để mô hình hóa các đối tượng phức tạp.
Hiệu ứng và kết cấu: Các hiệu ứng ánh sáng và kết cấu trên khối lập phương giúp tạo nên hình ảnh chân thực và sinh động trong các trò chơi điện tử và phim hoạt hình.
Hình học và toán học
Giáo dục và giảng dạy: Khối lập phương là một công cụ trực quan giúp học sinh hiểu về các khái niệm hình học cơ bản như thể tích, diện tích và tính đối xứng.
Nghiên cứu toán học: Khối lập phương thường được sử dụng trong các nghiên cứu toán học về hình học không gian và các tính chất liên quan.
Kỹ thuật và công nghệ
Sản xuất và gia công: Trong ngành công nghiệp, khối lập phương được sử dụng để sản xuất và gia công các sản phẩm nhờ vào tính dễ dàng trong việc tính toán và chế tạo.
Thiết kế cơ khí: Nhiều bộ phận máy móc và thiết bị kỹ thuật được thiết kế dưới dạng khối lập phương để dễ dàng lắp ráp và bảo trì.
Ứng dụng thực tế và đời sống
Đồ chơi và trò chơi: Khối lập phương là dạng cơ bản của nhiều loại đồ chơi như khối xếp hình, trò chơi ghép hình và các loại đồ chơi phát triển trí tuệ khác.
Thiết bị lưu trữ và sắp xếp: Các hộp lưu trữ và sắp xếp thường có dạng khối lập phương để tối ưu hóa không gian và dễ dàng trong việc sắp xếp.
Thiên văn học
Mô phỏng không gian: Khối lập phương được sử dụng trong các mô phỏng không gian và nghiên cứu về các cấu trúc vũ trụ nhờ vào khả năng chia nhỏ không gian thành các đơn vị dễ quản lý.
Nghệ thuật và thiết kế
Tác phẩm nghệ thuật: Nhiều tác phẩm nghệ thuật và thiết kế hiện đại sử dụng hình khối lập phương để tạo nên các tác phẩm sáng tạo và độc đáo.
Trang trí nội thất: Khối lập phương cũng được sử dụng trong trang trí nội thất để tạo ra các không gian sống gọn gàng và hiện đại.
Những ứng dụng đa dạng này cho thấy khối lập phương không chỉ là một khái niệm toán học đơn giản mà còn là một yếu tố quan trọng trong nhiều lĩnh vực của cuộc sống và công nghệ.
Bài tập vận dụng

Dưới đây là một số bài tập vận dụng về khối lập phương, từ cơ bản đến nâng cao, để giúp bạn hiểu rõ hơn về các tính chất và ứng dụng của khối lập phương.
Bài Tập 1: Tính diện tích toàn phần và thể tích
Bài toán
Cho một khối lập phương có cạnh dài 5 cm. Hãy tính diện tích toàn phần và thể tích của khối lập phương này.
Lời giải
Diện tích toàn phần \(S\)
\[ S = 6a^2 = 6 \times 5^2 = 6 \times 25 = 150 \text{ cm}^2 \]
Thể tích \(V\):
\[ V = a^3 = 5^3 = 125 \text{ cm}^3\]
Bài tập 2: Tính đường chéo mặt và đường chéo không gian
Bài toán
Một khối lập phương có chiều dài cạnh là 6 cm. Hãy tính độ dài đường chéo của một mặt và đường chéo không gian của khối lập phương.
Lời giải:
Đường chéo mặt \(d\):
\[d = a\sqrt{2} = 6\sqrt{2} \approx 8.49 \text{ cm} \]
Đường chéo không gian \(D\)
\[ D = a\sqrt{3} = 6\sqrt{3} \approx 10.39 \text{ cm}\]
Bài tập 3: Tính diện tích mặt bên
Bài toán
Khối lập phương có thể tích là 64 cm³. Hãy tính diện tích của một mặt bên của khối lập phương.
Lời giải
Diện tích một mặt bên \(A\)
\[ A = a^2 = 4^2 = 16 \text{ cm}^2 \]
Bài tập 4: Ứng dụng thực tế
Bài toán
Một bể chứa nước hình lập phương có cạnh dài 2 m. Nếu bể này được làm đầy nước, hãy tính khối lượng nước mà bể chứa được (biết rằng 1 m³ nước nặng 1000 kg).
Lời giải
Thể tích của bể chứa
\[V = a^3 = 2^3 = 8 \text{ m}^3 \]
Khối lượng nước
\[ Khối lượng = V \times 1000 = 8 \times 1000 = 8000 \text{ kg} \]
Bài Tập 5: Tính tỷ lệ thể tích
Bài toán
Hai khối lập phương có cạnh lần lượt là 3 cm và 6 cm. Hãy tính tỷ lệ thể tích của hai khối lập phương này.
Lời giải
Thể tích khối lập phương nhỏ \(V_1\)
\[ V_1 = 3^3 = 27 \text{ cm}^3\]
Thể tích khối lập phương lớn \(V_2\):
\[ V_2 = 6^3 = 216 \text{ cm}^3 \]
Tỷ lệ thể tích
\[Tỷ lệ = \frac{V_2}{V_1} = \frac{216}{27} = 8\]
Những bài tập này giúp bạn rèn luyện khả năng tính toán và hiểu rõ hơn về các tính chất của khối lập phương, từ đó có thể ứng dụng vào các bài toán thực tế và các lĩnh vực khác nhau.
Qua những bài tập và ứng dụng đã được trình bày, chúng ta đã thấy rõ tầm quan trọng và sự đa dạng của khối lập phương trong nhiều lĩnh vực từ toán học, kiến trúc, kỹ thuật đến đời sống hàng ngày. Khối lập phương không chỉ là một khái niệm hình học cơ bản mà còn là một công cụ hữu ích giúp chúng ta giải quyết nhiều vấn đề thực tế và phát triển những ứng dụng công nghệ tiên tiến. Hy vọng rằng thông qua việc tìm hiểu và áp dụng các công thức và tính chất của khối lập phương, bạn đã có thêm kiến thức và sự tự tin để tiếp tục khám phá những bài toán và thách thức mới.