Định nghĩa số chính phương là gì? Tính chất và ví dụ minh họa

Trong toán học, khái niệm về số chính phương là một trong những điều cơ bản và quan trọng. Để hiểu rõ hơn về số chính phương, chúng ta cần tìm hiểu về định nghĩa của nó, cũng như những tính chất và ví dụ minh họa để áp dụng trong thực tế.

Định nghĩa số chính phương 

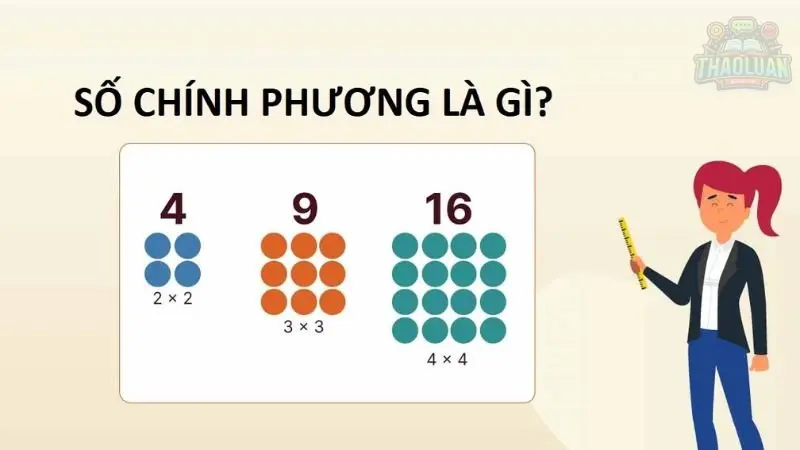
Số chính phương là một số nguyên dương mà căn bậc hai của nó cũng là một số nguyên dương. Nói cách khác, một số nguyên dương \(n\) được gọi là số chính phương nếu tồn tại một số nguyên dương \(m\) sao cho \(n = m^2\).

Công thức

Công thức để tính số chính phương là:

\[ n = m^2 \]

Trong đó

\( n \) là số chính phương.

\( m \) là căn bậc hai của \( n \), cũng là một số nguyên.

Ví dụ minh họa

Số 4 là một số chính phương vì \(4 = 2^2\).

Số 9 cũng là một số chính phương vì \(9 = 3^2\).

Số 16 là số chính phương vì \(16 = 4^2\).

Số 25 cũng là số chính phương vì \(25 = 5^2\).

Số 36 là số chính phương vì \(36 = 6^2\).

Những số chính phương này thường xuất hiện trong nhiều lĩnh vực toán học, từ lý thuyết số đến hình học và thậm chí trong các ứng dụng thực tế như trong thiết kế đường phố hoặc bố trí các ô vuông trong bảng số. Đặc biệt, các số chính phương cũng đóng vai trò quan trọng trong mật mã học và trong việc phân tích phổ của sóng âm thanh và sóng điện từ.

Đặc điểm của số chính phương

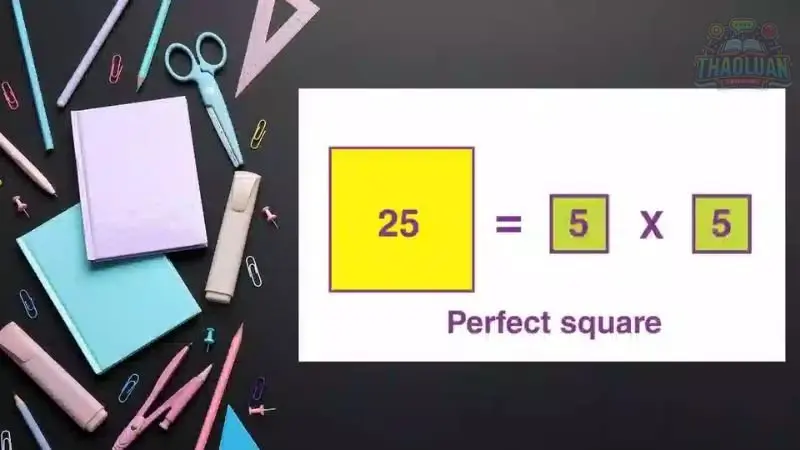
Là số nguyên dương: Số chính phương luôn là một số nguyên dương vì căn bậc hai của nó là một số nguyên dương.

Căn bậc hai nguyên tố: Một số chính phương có thể có căn bậc hai là một số nguyên tố hoặc không phải là số nguyên tố. Ví dụ, \(4\) là số chính phương và căn bậc hai của nó là \(2\), một số nguyên tố. Trong khi đó, \(6\) cũng là số chính phương, nhưng căn bậc hai của nó là một số không phải là số nguyên tố, \(2.449\).

Kết quả của phép nhân hai số nguyên: Một số chính phương thường được tạo ra bằng cách nhân hai số nguyên. Ví dụ, \(25\) là kết quả của \(5 \times 5\), \(36\) là kết quả của \(6 \times 6\).

Có thể được biểu diễn bằng hình vuông: Số chính phương có thể được biểu diễn bằng một hình vuông với số lượng đơn vị bằng căn bậc hai của số đó. Ví dụ, \(25\) có thể được biểu diễn bằng một hình vuông với kích thước \(5 \times 5\), \(36\) có thể được biểu diễn bằng một hình vuông với kích thước \(6 \times 6\).

Dễ dàng nhận diện: Một số chính phương có thể được nhận diện dễ dàng bằng cách kiểm tra xem căn bậc hai của nó có phải là một số nguyên hay không. Nếu căn bậc hai của một số là một số nguyên, thì số đó là số chính phương.

Những đặc điểm này giúp ta dễ dàng nhận diện và làm việc với các số chính phương trong nhiều tình huống toán học và thực tiễn.

Ví dụ về số chính phương

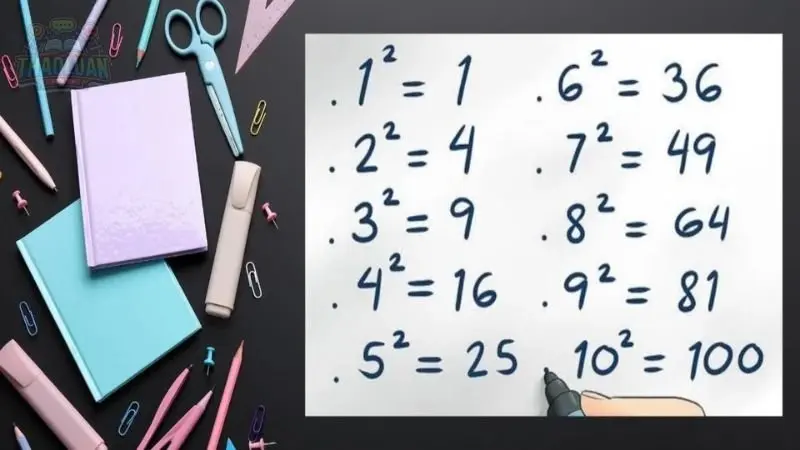
Dưới đây là một số ví dụ về các số chính phương và cách chúng được tạo ra:

\( 4 \): \(4\) là số chính phương vì \(2 \times 2 = 4\). Nó cũng có thể được biểu diễn bằng một hình vuông với các cạnh có độ dài bằng \(2\).

\( 9 \): \(9\) là số chính phương vì \(3 \times 3 = 9\). Đây cũng là một số nguyên tố. Một hình vuông với cạnh có độ dài bằng \(3\) sẽ có diện tích là \(9\).

\( 16 \): \(16\) là số chính phương vì \(4 \times 4 = 16\). Đây cũng là một số có căn bậc hai là một số nguyên tố. Một hình vuông với cạnh có độ dài bằng \(4\) sẽ có diện tích là \(16\).

\( 25 \): \(25\) là số chính phương vì \(5 \times 5 = 25\). Đây cũng là một số có căn bậc hai là một số nguyên tố. Một hình vuông với cạnh có độ dài bằng \(5\) sẽ có diện tích là \(25\).

\( 36 \): \(36\) là số chính phương vì \(6 \times 6 = 36\). Đây không phải là một số nguyên tố nhưng có căn bậc hai là một số nguyên. Một hình vuông với cạnh có độ dài bằng \(6\) sẽ có diện tích là \(36\).

Các ví dụ trên là một số trong những số chính phương đầu tiên và đơn giản nhất. Trong toán học, số chính phương còn được sử dụng rộng rãi trong nhiều bài toán và ứng dụng khác nhau.

Số chính phương nhỏ nhất 

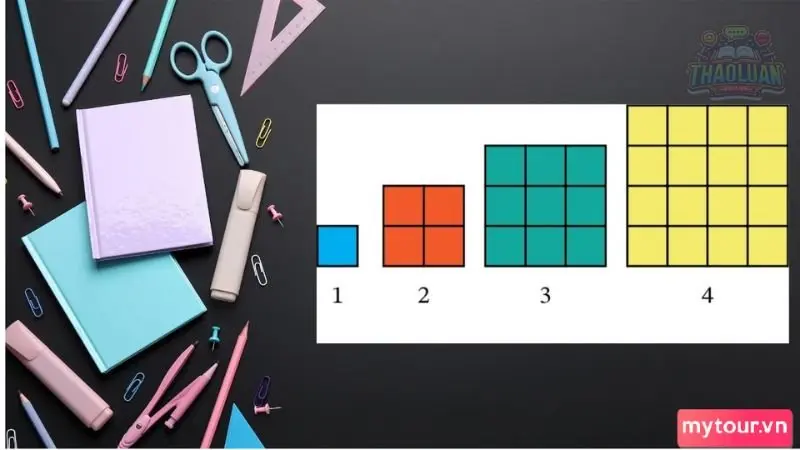
Số chính phương nhỏ nhất là số chính phương có giá trị nhỏ nhất.

Nếu chỉ xét các số tự nhiên dương, thì số chính phương nhỏ nhất là 1. Vì 1 có thể biểu diễn dưới dạng bình phương của 1, tức là \(1^2 = 1\).

Tuy nhiên, nếu xét tất cả các số tự nhiên, bao gồm cả số 0, thì số chính phương nhỏ nhất là 0. Vì 0 có thể biểu diễn dưới dạng bình phương của 0, tức là \(0^2 = 0\).

Ví dụ

\(1\) là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của \(1\), tức là \(1^2 = 1\).

\(4\) là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của \(2\), tức là \(2^2 = 4\).

\(9\) là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của \(3\), tức là \(3^2 = 9\).

\(16\) là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của \(4\), tức là \(4^2 = 16\).

\(0\) là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của \(0\), tức là \(0^2 = 0\).

(1) là số chính phương vì nó có thể biểu diễn dưới dạng bình phương của (1), tức là (1^2 = 1).

Số chính phương lớn nhất trong phạm vi nguyên tố

Số chính phương là số nguyên dương có thể được biểu diễn dưới dạng bình phương của một số nguyên dương khác. Ví dụ: \(4\), \(9\), \(16\), \(25\), \(36\), \(49\), \(64\), \(81\), \(100\) đều là số chính phương.

Mỗi phạm vi số nguyên tố, số chính phương lớn nhất được xác định bằng cách tính bình phương của số nguyên tố lớn nhất trong phạm vi đó.

Ví dụ

Phạm vi số nguyên tố  1 chữ số (từ 1 đến 9), số nguyên tố lớn nhất là \(3\). Do đó, số chính phương lớn nhất trong phạm vi này là \(9\) (bình phương của \(3\)).

Trong phạm vi số nguyên tố có 2 chữ số (từ 10 đến 99), số nguyên tố lớn nhất là \(97\). Do đó, số chính phương lớn nhất trong phạm vi này là \(9409\) (bình phương của \(97\)).

Trong phạm vi số nguyên tố có 3 chữ số (từ 100 đến 999), số nguyên tố lớn nhất là \(997\). Do đó, số chính phương lớn nhất trong phạm vi này là \(994009\) (bình phương của \(997\)).

Trong phạm vi số nguyên tố có 4 chữ số (từ 1000 đến 9999), số nguyên tố lớn nhất là \(9973\). Do đó, số chính phương lớn nhất trong phạm vi này là \(99430049\) (bình phương của \(9973\)).

Trong phạm vi số nguyên tố có 5 chữ số (từ 10000 đến 99999), số nguyên tố lớn nhất là \(99991\). Do đó, số chính phương lớn nhất trong phạm vi này là \(999820081\) (bình phương của \(99991\)).

Số chính phương lớn nhất trong phạm vi số nguyên tố có \(n\) chữ là bình phương của số nguyên tố lớn nhất có \(n\) chữ số.

Cách tính số chính phương

Để tính toán một số có phải là số chính phương hay không, bạn có thể sử dụng một số phương pháp khác nhau, nhưng cách đơn giản nhất là kiểm tra xem căn bậc hai của số đó có phải là một số nguyên hay không. Nếu căn bậc hai của số đó là một số nguyên, thì số đó là số chính phương. Dưới đây là cách tính số chính phương theo phương pháp này

Tính căn bậc hai của số đó

Cho một số nguyên dương \(n\), tính căn bậc hai của \(n\).

Nếu căn bậc hai của \(n\) là một số nguyên, tiến hành bước tiếp theo.

Kiểm tra kết quả

Nếu căn bậc hai của \(n\) là một số nguyên, thì \(n\) là số chính phương.

Nếu căn bậc hai của \(n\) không phải là một số nguyên, thì \(n\) không phải là số chính phương.

Ví dụ, để kiểm tra xem số \(25\) có phải là số chính phương hay không:

Tính căn bậc hai của Số 25: 

Căn bậc hai của \(25\) là \(5\), vì \(5 \times 5 = 25\).

Kiểm tra kết quả 

Vì căn bậc hai của \(25\) là một số nguyên (tức là \(5\)), nên \(25\) là số chính phương.

Để kiểm tra xem một số có phải là số chính phương hay không, bạn chỉ cần tính căn bậc hai của số đó và kiểm tra xem kết quả có phải là một số nguyên hay không.

Ý nghĩa của số chính phương trong toán học

Số chính phương có ý nghĩa quan trọng trong toán học với nhiều ứng dụng và tính chất đặc biệt:

Trong lý thuyết số: Số chính phương là một lĩnh vực quan trọng trong lý thuyết số, nơi nó đóng vai trò quan trọng trong việc nghiên cứu các thuật toán liên quan đến phân tích số học, như phân tích số nguyên tố và phân tích tổ hợp.

Trong hình học: Số chính phương liên quan chặt chẽ đến hình học vì chúng thường được biểu diễn bằng các hình vuông. Điều này có thể có ứng dụng trong việc tính diện tích, chu vi và các vấn đề liên quan đến hình học khác.

Trong mật mã học: Số chính phương cũng có ứng dụng trong mật mã học, nơi chúng có thể được sử dụng trong việc tạo các hàm băm và các hệ thống mã hóa dựa trên toán học.

Trong kỹ thuật điện: Trong kỹ thuật điện, số chính phương có thể xuất hiện trong việc tính toán điện áp, dòng điện và điện trở, đặc biệt là trong các mạch điện đơn giản.

Trong khoa học máy tính: Trong khoa học máy tính, số chính phương có thể được sử dụng trong việc tạo ra các cấu trúc dữ liệu hiệu quả và trong việc thiết kế các thuật toán hiệu quả cho các vấn đề tính toán.

Trong vật lý:  Trong vật lý, số chính phương có thể xuất hiện trong nhiều vấn đề liên quan đến cơ học lượng tử và lý thuyết trường lượng tử, cũng như trong việc mô hình hóa các quá trình vật lý khác.

Số chính phương không chỉ là một khái niệm toán học cơ bản mà còn có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của khoa học và công nghệ. Điều này làm cho nó trở thành một phần quan trọng của nền tảng toán học và có giá trị trong nghiên cứu và ứng dụng thực tiễn.

Các đặc tính cơ bản của số chính phương 

Luôn là số nguyên dương: Số chính phương luôn là một số nguyên dương vì nó là kết quả của một bình phương.

Có thể biểu diễn bằng hình vuông: Số chính phương có thể được biểu diễn bằng một hình vuông với cạnh có độ dài bằng căn bậc hai của số đó.

Là kết quả của phép nhân hai số nguyên: Một số chính phương thường là kết quả của việc nhân hai số nguyên với nhau. Ví dụ, \(25\) là kết quả của \(5 \times 5\), \(36\) là kết quả của \(6 \times 6\).

Có căn bậc hai là một số nguyên: Một đặc điểm quan trọng của số chính phương là căn bậc hai của nó luôn là một số nguyên. Ví dụ, căn bậc hai của \(25\) là \(5\), một số nguyên.

Không phải tất cả các số chính phương đều là số nguyên tố: Mặc dù một số chính phương như \(4\) và \(9\) là số nguyên tố, nhưng không phải tất cả các số chính phương đều là số nguyên tố. Ví dụ, \(6\) và \(8\) đều là số chính phương nhưng không phải là số nguyên tố.

Có số lượng hữu hạn số chính phương trong mỗi phạm vi: Trong mỗi phạm vi số nguyên, chỉ có một số hữu hạn các số chính phương. Điều này có nghĩa là không có vô hạn số chính phương trong một phạm vi nhất định.

Có sự liên kết với hệ số Euler-Mascheroni: Số chính phương có mối liên kết với hệ số Euler-Mascheroni, một hằng số quan trọng trong lý thuyết số.

Những đặc tính này là những đặc điểm cơ bản và quan trọng của số chính phương, và chúng giúp chúng ta hiểu rõ hơn về tính chất và ứng dụng của chúng trong toán học và thực tế.

Một số dạng bài tập về số chính phương

Dưới đây là một bài tập vận dụng về số chính phương

Bài tập: Hãy tìm số chính phương nhỏ nhất lớn hơn \(1000\) và chia hết cho \(12\).

Giải

Tìm số chính phương lớn nhất không vượt quá \(1000\).

Số chính phương lớn nhất không vượt quá \(1000\) là \(31^2 = 961\).

Tìm số chính phương lớn nhất từ \(961\) đến \(1000\) và chia hết cho \(12\).

Số chính phương lớn nhất từ \(961\) đến \(1000\) là \(31^2 = 961\).

Chia \(961\) cho \(12\), ta được kết quả là \(80.0833\). Do đó, số chính phương lớn nhất từ \(961\) đến \(1000\) và chia hết cho \(12\) là \(961\).

Tìm số chính phương lớn nhất từ \(1001\) trở đi và chia hết cho \(12\).

Số chính phương tiếp theo sau \(961\) là \(32^2 = 1024\).

Chia \(1024\) cho \(12\), ta được kết quả là \(85.3333\). Do đó, số chính phương lớn nhất từ \(1001\) trở đi và chia hết cho \(12\) là \(1024\).

Trong bài tập này, chúng ta đã áp dụng kiến thức về số chính phương và phép chia để tìm ra một số cụ thể đáp ứng yêu cầu của đề bài. Qua quá trình giải bài tập, chúng ta đã thấy sự áp dụng linh hoạt của kiến thức toán học trong việc giải quyết các vấn đề thực tế.

Hy vọng rằng việc thực hành này đã giúp bạn nắm vững hơn về số chính phương và phát triển kỹ năng suy luận và logic trong quá trình giải quyết bài toán. Nếu bạn có bất kỳ câu hỏi nào khác hoặc cần thêm sự giúp đỡ, đừng ngần ngại để lại cho tôi biết.