Định nghĩa tam giác cân là gì? Tính chất của tam giác cân

Trong hình học, tam giác cân là một khái niệm quen thuộc và quan trọng. Với đặc điểm đặc biệt và tính chất độc đáo, tam giác cân không chỉ là một hình học đơn giản mà còn là nền tảng cho nhiều khái niệm và bài toán phức tạp hơn. Trong phần này, chúng ta sẽ cùng tìm hiểu về định nghĩa và các tính chất của tam giác cân, từ những khái niệm cơ bản đến những ứng dụng thực tiễn.Hãy cùng nhau khám phá về tam giác cân, một trong những khái niệm căn bản và quan trọng nhất trong hình học.

Định nghĩa tam giác cân

Định nghĩa tam giác cân là một loại tam giác trong hình học có hai cạnh đối xứng nhau, còn được gọi là các cạnh cân, và hai góc tương ứng với các cạnh cân cũng bằng nhau. Trong một tam giác cân, các đỉnh của tam giác nằm trên một đường trung trực của cạnh cân tương ứng. Điều này có nghĩa là đường cao kẻ từ đỉnh của tam giác đến cạnh cần sẽ chia cạnh đó thành hai phần bằng nhau. Tam giác cân là một khái niệm quan trọng trong hình học và được sử dụng rộng rãi trong nhiều bài toán và ứng dụng thực tế.

Phân loại tam giác cân 

Tam giác cân có thể được phân loại dựa trên các đặc điểm khác nhau, bao gồm:

Phân loại dựa trên góc

Tam giác cân vuông: Một trong ba góc của tam giác là góc vuông.

Tam giác cân nhọn: Tất cả ba góc của tam giác đều nhọn.

Tam giác cân tù: Tất cả ba góc của tam giác đều tù.

Phân loại dựa trên cạnh

Tam giác cân đều: Cả ba cạnh của tam giác cân đều bằng nhau.

Tam giác cân không đều: Có hai cạnh của tam giác cân bằng nhau.

Phân loại dựa trên chiều dài cạnh

Tam giác cân có cạnh bằng: Hai cạnh đối xứng của tam giác cân có độ dài bằng nhau.

Tam giác cân không có cạnh bằng: Hai cạnh đối xứng của tam giác cân không có độ dài bằng nhau.

Phân loại dựa trên độ dài cao

Tam giác cân có chiều cao bằng: Cao của tam giác cân đo từ đỉnh đến cạnh đối xứng có độ dài bằng nhau.

Tam giác cân không có chiều cao bằng: Cao của tam giác cân không đo từ đỉnh đến cạnh đối xứng có độ dài bằng nhau.

Phân loại này giúp xác định và phân biệt các loại tam giác cân dựa trên các đặc điểm khác nhau của chúng.

Các yếu tố của tam giác cân

Các yếu tố chính của tam giác cân bao gồm:

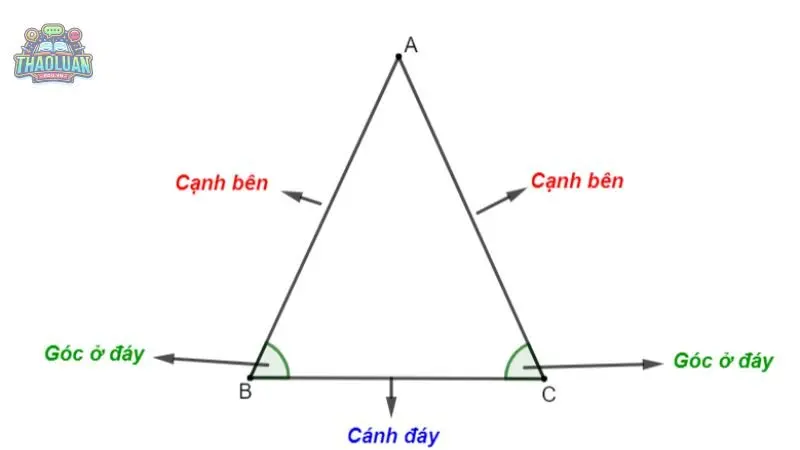
Cạnh cân: Hai cạnh bằng nhau của tam giác cân được gọi là các cạnh cân.

Đây là đặc điểm đặc trưng nhất giúp phân biệt tam giác cân với các loại tam giác khác.

Đáy: Cạnh còn lại của tam giác cân, không bằng với hai cạnh cân, được gọi là cạnh đáy.

Góc cân: Hai góc đối diện với hai cạnh cân có độ lớn bằng nhau.

Các góc này được gọi là các góc cân.

Góc đỉnh: Góc nằm giữa hai cạnh cân, đối diện với cạnh đáy, được gọi là góc đỉnh.

Đây là góc duy nhất không bằng với hai góc cân.

Đường cao: Đường cao trong tam giác cân là đoạn thẳng kẻ từ đỉnh xuống vuông góc với cạnh đáy.

Đường cao này không chỉ chia cạnh đáy thành hai đoạn bằng nhau mà còn chia tam giác cân thành hai tam giác vuông bằng nhau.

Trục đối xứng: Tam giác cân có một trục đối xứng, đó là đường thẳng đi qua đỉnh và trung điểm của cạnh đáy.

Trục đối xứng này chia tam giác cân thành hai phần bằng nhau.

Đường trung tuyến: Đường trung tuyến trong tam giác cân là đoạn thẳng nối từ đỉnh đến trung điểm của cạnh đáy.

Đường trung tuyến này cũng là đường cao và đường phân giác của góc đỉnh.

Đường phân giác: Đường phân giác của góc đỉnh cũng chính là đường cao và đường trung tuyến, chia góc đỉnh thành hai phần bằng nhau và chia tam giác cân thành hai tam giác vuông bằng nhau.

Các yếu tố này giúp xác định các đặc điểm và tính chất cơ bản của tam giác cân, từ đó giúp hiểu rõ hơn về hình dạng và các tính chất toán học của nó.

Tính chất của tam giác cân

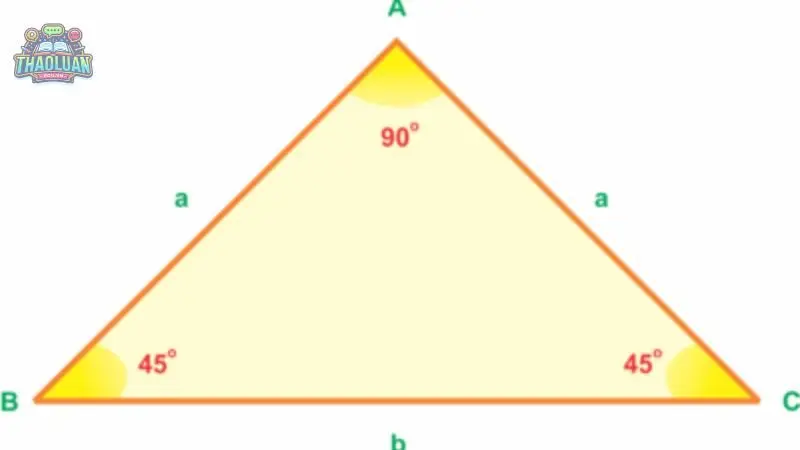
Tam giác cân có một số tính chất đặc biệt, giúp phân biệt nó với các loại tam giác khác. Dưới đây là các tính chất quan trọng của tam giác cân:

Hai cạnh bằng nhau: Hai cạnh bên của tam giác cân có độ dài bằng nhau.

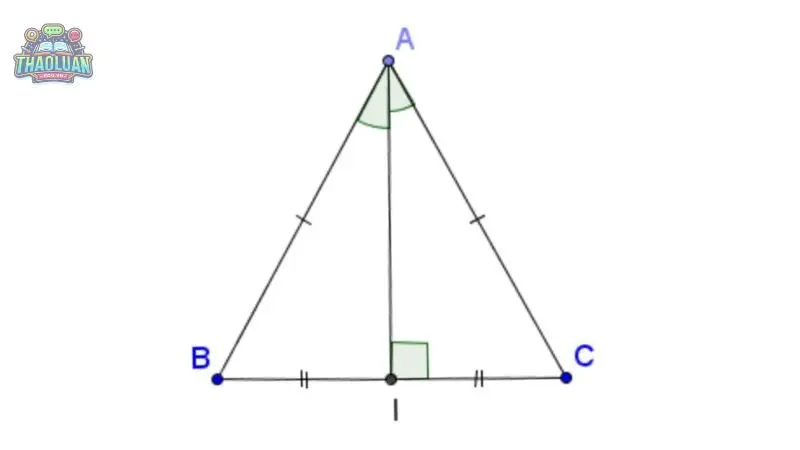
Trục đối xứng: Tam giác cân có một trục đối xứng đi qua đỉnh và trung điểm của cạnh đáy. Trục đối xứng này chia tam giác thành hai tam giác vuông bằng nhau.

Đường cao, đường trung tuyến, và đường phân giác

Đường cao kẻ từ đỉnh xuống trung điểm của cạnh đáy cũng đồng thời là đường trung tuyến và đường phân giác của góc ở đỉnh. Điều này có nghĩa là:

Đường cao chia tam giác thành hai tam giác vuông bằng nhau.

Đường trung tuyến chia cạnh đáy thành hai đoạn bằng nhau.

Đường phân giác chia góc đỉnh thành hai góc bằng nhau.

Chu vi

Chu vi của tam giác cân được tính bằng tổng độ dài của tất cả các cạnh.

\[ P = a + 2b \]

Trong đó \(a\) là độ dài của cạnh đáy và \(b\) là độ dài của hai cạnh bên.

Diện tích

Diện tích của tam giác cân được tính bằng công thức:

\[ S = \frac{1}{2} \times a \times h \]

Trong đó \(a\) là độ dài của cạnh đáy và \(h\) là chiều cao từ đỉnh đến cạnh đáy.

Đường tròn ngoại tiếp và nội tiếp

Tam giác cân có thể nội tiếp và ngoại tiếp đường tròn. Tâm của đường tròn ngoại tiếp tam giác cân nằm trên trục đối xứng và là trung điểm của đường cao từ đỉnh đến cạnh đáy.

Tâm của đường tròn nội tiếp cùng nằm trên trục đối xứng và là điểm giao của các đường phân giác của các góc.

Tính chất góc

Nếu tam giác cân có một góc đỉnh bằng \(90^\circ\) thì tam giác đó là tam giác vuông cân.

Những tính chất này giúp nhận diện và giải quyết các bài toán liên quan đến tam giác cân, đồng thời cũng ứng dụng rộng rãi trong nhiều lĩnh vực như toán học, kiến trúc và kỹ thuật.

Ứng dụng của tam giác cân

Tam giác cân có nhiều ứng dụng trong các lĩnh vực khác nhau của cuộc sống và khoa học. Dưới đây là một số ứng dụng cụ thể của tam giác cân:

Kiến trúc và xây dựng

Mái nhà nhiều mái nhà được thiết kế dưới dạng tam giác cân để tạo độ dốc cần thiết cho việc thoát nước mưa và tuyết. Điều này giúp bảo vệ ngôi nhà khỏi thời tiết khắc nghiệt.

Cầu thang các bậc thang trong một số thiết kế cầu thang có thể sử dụng các tam giác cân để đảm bảo tính ổn định và thẩm mỹ.

Thiết kế đồ họa và nghệ thuật

Logo và biểu tượng nhiều logo và biểu tượng sử dụng tam giác cân để tạo ra hình ảnh cân đối và thu hút. Hình dạng đối xứng của tam giác cân tạo cảm giác ổn định và tin cậy.

Trang trí nội thất tam giác cân được sử dụng trong các thiết kế nội thất, như gương, khung ảnh, và đèn trang trí để tạo điểm nhấn thẩm mỹ.

Khoa học và kỹ thuật

Cấu trúc tòa nhà và cầu trong kỹ thuật xây dựng, tam giác cân được sử dụng trong thiết kế cấu trúc để phân bổ lực và đảm bảo tính ổn định. Các khung kim loại và dầm cầu thường có các tam giác cân để gia cố và chịu lực.

Công nghệ chế tạo tam giác cân cũng xuất hiện trong thiết kế máy móc và thiết bị để tạo sự cân bằng và tối ưu hóa lực phân bổ.

Toán học và giáo dục

Dạy học hình học tam giác cân là một chủ đề cơ bản trong giáo dục hình học, giúp học sinh hiểu về đối xứng, cân bằng và các tính chất hình học khác.

Bài tập và thực hành tam giác cân thường được sử dụng trong các bài toán và bài tập để rèn luyện kỹ năng giải toán và hiểu biết về các định lý hình học.

Thiên nhiên

Hình dạng của núi và đồi nhiều ngọn núi và đồi có hình dạng tương tự tam giác cân, với đỉnh nhọn và hai cạnh dốc đều nhau.

Hình dạng của cây cối một số loài cây, đặc biệt là cây thông, có hình dạng tam giác cân, giúp chúng phân bố đều ánh sáng và phát triển ổn định.

Biển báo giao thông

Biển báo nguy hiểm nhiều biển báo giao thông có hình dạng tam giác cân để cảnh báo người tham gia giao thông về các nguy hiểm phía trước. Hình dạng tam giác thu hút sự chú ý và truyền đạt thông tin một cách hiệu quả.

Những ứng dụng này cho thấy tam giác cân không chỉ là một khái niệm toán học mà còn là một phần quan trọng trong nhiều khía cạnh của cuộc sống và kỹ thuật. Việc hiểu rõ các tính chất và ứng dụng của tam giác cân giúp chúng ta áp dụng kiến thức này vào nhiều tình huống thực tế khác nhau.

Bài tập áp dụng cách chứng minh tam giác cân 

Dưới đây là một số bài tập nhằm giúp bạn áp dụng các tính chất và định lý liên quan đến tam giác cân, cùng với các bước chứng minh chi tiết.

Bài tập 1: Chứng minh tam giác cân

Đề bài: Cho tam giác ABC với AB = AC. Gọi D là điểm nằm trên cạnh BC sao cho AD là đường phân giác của góc BAC. Chứng minh rằng tam giác ABD và tam giác ACD bằng nhau, từ đó suy ra AD vuông góc với BC.

Lời giải:

Xét tam giác ABD và tam giác ACD:

AB = AC (giả thiết)

Góc BAD = góc CAD (AD là đường phân giác của góc BAC)

AD là cạnh chung

Do đó, theo định lý cạnh-góc-cạnh (c.g.c), ta có:

\[ \Delta ABD = \Delta ACD \]

Từ đó suy ra:

  BD = CD (các cạnh tương ứng bằng nhau)

  Góc ADB = góc ADC (các góc tương ứng bằng nhau)

Kết luận:

Vì góc ADB và góc ADC là hai góc kề bù (tổng bằng 180 độ), nên mỗi góc bằng 90 độ.

\[ \text{Do đó, AD vuông góc với BC} \]

Bài tập 2: Chứng minh tam giác cân

Đề bài: Cho tam giác ABC với AB = AC. Gọi M là trung điểm của BC. Chứng minh rằng AM là đường phân giác của góc BAC, đồng thời là đường cao và đường trung tuyến của tam giác ABC.

Lời giải:

Xét tam giác ABM và tam giác ACM:

    AB = AC (giả thiết)

    BM = CM (M là trung điểm của BC)

    AM là cạnh chung

Do đó, theo định lý cạnh-cạnh-cạnh (c.c.c), ta có:

\[ \Delta ABM = \Delta ACM \]

Từ đó suy ra:

   Góc BAM = góc CAM (các góc tương ứng bằng nhau)

   AM là đường phân giác của góc BAC

   Góc BMA = góc CMA (các góc tương ứng bằng nhau)

Kết luận:

Vì góc BMA và góc CMA là hai góc kề bù (tổng bằng 180 độ), nên mỗi góc bằng 90 độ.

\[ \text{Do đó, AM vuông góc với BC,} \]

\[ \text{vậy AM là đường cao của tam giác ABC.} \]

Đường trung tuyến:

Vì AM đi qua trung điểm của BC và là đường cao, nên AM cũng là đường trung tuyến của tam giác ABC.

Bài tập 3: Ứng dụng tam giác cân trong thực tế

Đề bài: Trong một khu vườn hình tam giác ABC, người ta trồng cây sao cho AB = AC. Người ta muốn xây dựng một đường đi thẳng từ đỉnh A đến cạnh BC, sao cho đường đi này vuông góc với BC. Chứng minh rằng đường đi này sẽ chia BC thành hai đoạn bằng nhau.

Lời giải:

Giả thiết:

AB = AC

Đường đi từ A vuông góc với BC

Chứng minh:

Gọi D là điểm mà đường đi từ A gặp BC.

Vì AD vuông góc với BC, nên tam giác ABD và tam giác ACD là hai tam giác vuông.

Xét tam giác ABD và tam giác ACD:

AB = AC (giả thiết)

AD là cạnh chung

Góc ADB = góc ADC = 90 độ (đường đi vuông góc với BC)

Do đó, theo định lý cạnh-góc-cạnh (c.g.c), ta có:

\[ \Delta ABD = \Delta ACD \]

Từ đó suy ra:

BD = CD (các cạnh tương ứng bằng nhau)

Kết luân:

Đường đi từ A vuông góc với BC chia BC thành hai đoạn bằng nhau, BD và CD.

Các bài tập trên giúp minh họa cách áp dụng định lý và tính chất của tam giác cân trong việc giải quyết các bài toán hình học. Việc hiểu và chứng minh các bài toán này giúp củng cố kiến thức và khả năng tư duy logic trong hình học.

Hy vọng qua bài viết này, bạn đã có một cái nhìn tổng quan và hiểu rõ hơn về định nghĩa, tính chất và ứng dụng của tam giác cân. Tam giác cân không chỉ là một khái niệm cơ bản trong hình học mà còn có nhiều ứng dụng thực tế trong cuộc sống và các lĩnh vực khoa học khác. Việc nắm vững các kiến thức về tam giác cân sẽ giúp bạn giải quyết các bài toán hình học một cách dễ dàng và hiệu quả hơn.

Cảm ơn bạn đã dành thời gian theo dõi và đọc bài viết. Chúng tôi mong rằng những thông tin này sẽ hữu ích và góp phần vào sự thành công trong học tập và công việc của bạn. Nếu có bất kỳ câu hỏi hay thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được giải đáp thêm. Chúc bạn học tập tốt và thành công! Hãy theo dõi trang thaoluan,edu.vn nhé!