Định nghĩa tích phân và các phương pháp tính tích phân cơ bản 

Tích phân – một trong những khái niệm cơ bản và quan trọng nhất trong toán học – đóng vai trò quan trọng trong việc giải quyết nhiều vấn đề phức tạp của thế giới thực. Tích phân không chỉ là công cụ mạnh mẽ để tính toán diện tích, thể tích và các đại lượng vật lý khác, mà còn là nền tảng của nhiều lĩnh vực khác nhau như vật lý, kinh tế, và khoa học máy tính. Trong bài viết này, chúng ta sẽ khám phá định nghĩa của tích phân cùng với các phương pháp tính tích phân cơ bản để hiểu rõ hơn về tầm quan trọng và ứng dụng của nó trong thế giới thực.

Định nghĩa tích phân Riemann – Riemann

Tích phân Riemann là một khái niệm quan trọng trong toán học, được đặt tên theo nhà toán học Bernhard Riemann. Tích phân Riemann cung cấp một cách tiếp cận toán học để hiểu diện tích dưới đường cong phức tạp và là một phần quan trọng của lý thuyết tích phân.

Theo định nghĩa, tích phân Riemann của một hàm số \( f(x) \) trên một khoảng \( [a, b] \) được xác định bằng cách chia khoảng này thành các phần nhỏ, gọi là các đoạn, sau đó tính tổng của các giá trị của hàm số trên mỗi đoạn và nhân với chiều dài của đoạn đó. Khi kích thước của các đoạn tiến dần về 0, giá trị của tổng này tiến gần đến một giá trị cố định, gọi là tích phân của \( f(x) \) trên khoảng \( [a, b] \).

Tích phân Riemann cung cấp một cách tiếp cận mạnh mẽ để hiểu các khái niệm như diện tích dưới đường cong, tổng phân phối, và tổng tiền đề, và là nền tảng của nhiều phương pháp tính tích phân trong toán học và ứng dụng thực tế.

Công thức tính tích phân 

Tích phân là một khái niệm quan trọng trong toán học, đặc biệt là trong giải tích. Nó được sử dụng để tính diện tích dưới một đường cong, tổng của một hàm theo thời gian, hoặc nhiều ứng dụng khác trong vật lý và kỹ thuật. Dưới đây là một số công thức tích phân cơ bản:

Tích phân xác định

Tích phân xác định của một hàm số \( f(x) \) trong khoảng từ \( a \) đến \( b \) được ký hiệu là:

\[ \int_{a}^{b} f(x) \, dx \]

Điều này biểu thị diện tích dưới đường cong của hàm số \( f(x) \) từ \( x = a \) đến \( x = b \).

Tích phân bất định

Tích phân bất định của một hàm số \( f(x) \) là:

\[ \int f(x) \, dx = F(x) + C \]

Trong đó \( F(x) \) là nguyên hàm của \( f(x) \) và \( C \) là hằng số tích phân.

Các công thức tích phân cơ bản

Tích phân của hàm số mũ:

\[ \int e^x \, dx = e^x + C \]

Tích phân của hàm số đa thức

\[ \int x^n \, dx = \frac{x^{n+1}}{n+1} + C \quad (n \neq -1) \]

Tích phân của hàm số lượng giác

\[ \int \sin(x) \, dx = -\cos(x) + C \]

\[ \int \cos(x) \, dx = \sin(x) + C \]

Tích phân của hàm số logarit:

\[ \int \frac{1}{x} \, dx = \ln|x| + C \]

Công thức tính tích phân theo định lý cơ bản của giải tích

Định lý cơ bản của giải tích liên kết tích phân xác định và tích phân bất định:

\[ \int_{a}^{b} f(x) \, dx = F(b) – F(a) \]

Trong đó \( F(x) \) là một nguyên hàm của \( f(x) \).

Tích phân từng phần

Tích phân từng phần là một công cụ hữu ích để giải quyết tích phân của các tích của hàm số:

\[ \int u \, dv = uv – \int v \, du \]

Trong đó \( u \) và \( v \) là các hàm số của \( x \).

Tích phân đổi biến số

Phương pháp đổi biến số giúp đơn giản hóa tích phân:

\[ \int f(g(x)) \cdot g'(x) \, dx = \int f(u) \, du \]

Trong đó \( u = g(x) \).

Các công thức này cung cấp một nền tảng vững chắc để giải quyết nhiều loại tích phân khác nhau trong toán học và các lĩnh vực liên quan.

Các tính chất của tích phân Riemann – Riemann

Tích phân Riemann là một khái niệm quan trọng trong toán học, đặc biệt trong lĩnh vực phân tích thực và toán hàm phức. Dưới đây là một số tính chất cơ bản của tích phân Riemann:

Định nghĩa: Tích phân Riemann của một hàm f(x) trên một đoạn [a, b] là một giới hạn của tổng các tích của giá trị của hàm f(x) tại các điểm lấy từ một phân đoạn của [a, b], khi kích thước của các phân đoạn này tiến tới 0.

Phụ thuộc vào phân đoạn: Giá trị của tích phân Riemann phụ thuộc vào cách chọn các điểm mẫu trong phân đoạn.

Tính chất tuyến tính: Tích phân của tổng hai hàm bằng tổng của tích phân của từng hàm đó.

Tính chất của hàm đơn điệu: Nếu f(x) ≤ g(x) trên [a, b], thì tích phân của f(x) trên [a, b] sẽ nhỏ hơn hoặc bằng tích phân của g(x) trên [a, b].

Tính chất của hàm không âm: Nếu f(x) ≥ 0 trên [a, b], thì tích phân của f(x) trên [a, b] là không âm.

Tính chất về tích phân của hàm nghịch đảo: Nếu f(x) không đổi dấu trên [a, b], thì tích phân của nó cũng sẽ không đổi dấu.

Tính chất về tổng địa phương: Nếu hàm f(x) liên tục trên [a, b], thì tích phân của nó trên [a, b] có thể tính bằng tổng của giá trị của hàm trên các điểm của [a, b].

Tính chất của các hàm mũ và sin, cos: Tích phân của các hàm mũ và các hàm chu kỳ trên một khoảng xác định có thể được tính chính xác hoặc gần đúng bằng các phương pháp cụ thể.

Những tính chất này cùng với những kiến thức về giới hạn và liên tục là những công cụ quan trọng trong việc tính toán và hiểu sâu về tích phân Riemann.

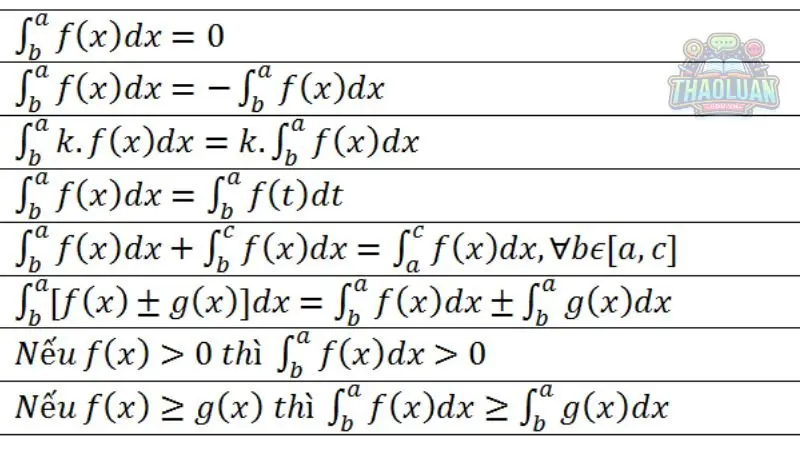
Ứng dụng của tích phân Riemann – Riemann

Tích phân Riemann có rất nhiều ứng dụng trong nhiều lĩnh vực khác nhau của toán học, khoa học và kỹ thuật. Dưới đây là một số ứng dụng phổ biến của tích phân Riemann:

Tính toán diện tích và thể tích: Tích phân Riemann được sử dụng để tính diện tích dưới đường cong và thể tích của các hình dạng phức tạp. Đây là ứng dụng cơ bản nhất và quan trọng nhất của tích phân Riemann.

Tính toán tốc độ và gia tốc: Trong vật lý, tích phân Riemann được sử dụng để tính toán tốc độ và gia tốc từ biểu đồ vị trí và biểu đồ vận tốc của vật.

Tính toán khối lượng và trọng lượng: Tích phân Riemann cũng được sử dụng để tính toán khối lượng của các vật thể có hình dạng phức tạp, cũng như trọng lượng của chúng dựa trên mật độ và trọng lực.

Tính toán lượng nhiệt và năng lượng: Trong vật lý và kỹ thuật, tích phân Riemann được sử dụng để tính toán lượng nhiệt và năng lượng trong các hệ thống phức tạp, như hệ thống dẫn nhiệt và hệ thống động cơ.

Tính toán xác suất và thống kê: Trong xác suất và thống kê, tích phân Riemann được sử dụng để tính toán xác suất và kỳ vọng của biến ngẫu nhiên trong các phân phối xác suất khác nhau.

Tính toán điểm trung bình và trọng tâm: Tích phân Riemann được sử dụng để tính toán điểm trung bình và trọng tâm của các hình dạng phức tạp, giúp trong việc định vị trọng tâm của vật thể.

Tính toán trong lý thuyết số và phân tích: Tích phân Riemann cũng được sử dụng trong lý thuyết số và phân tích số để tính toán các hàm số đặc biệt và tính toán các dãy vô hạn.

Các ứng dụng này chỉ là một phần nhỏ của cách mà tích phân Riemann được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau của khoa học và kỹ thuật.

Ví dụ về tích phân Riemann – Riemann

Ví dụ 1: Tính tích phân xác định của hàm số \( f(x) = x^2 \) từ \( x = 1 \) đến \( x = 3 \)

Bước 1: Xác định hàm số và khoảng tích phân

Hàm số: \( f(x) = x^2 \)

Khoảng tích phân: từ \( x = 1 \) đến \( x = 3 \)

Bước 2: Tìm nguyên hàm của \( f(x) \)

Nguyên hàm của \( x^2 \) là:

\[ \int x^2 \, dx = \frac{x^3}{3} + C \]

Bước 3: Áp dụng công thức tính tích phân xác định

Sử dụng định lý cơ bản của giải tích:

\[ \int_{1}^{3} x^2 \, dx = \left[ \frac{x^3}{3} \right]_{1}^{3} \]

Bước 4: Tính giá trị tại các điểm giới hạn

\[ \left[ \frac{x^3}{3} \right]_{1}^{3} = \frac{3^3}{3} – \frac{1^3}{3} \]

\[ = \frac{27}{3} – \frac{1}{3} \]

\[ = 9 – \frac{1}{3} \]

\[ = \frac{27}{3} – \frac{1}{3} \]

\[ = \frac{26}{3} \]

Kết quả

\[ \int_{1}^{3} x^2 \, dx = \frac{26}{3} \]

Ví dụ 2: Tích phân bất định của hàm số \( f(x) = \sin(x) \)

Bước 1: Xác định hàm số

Hàm số: \( f(x) = \sin(x) \)

Bước 2: Tìm nguyên hàm của \( f(x) \)

Nguyên hàm của \( \sin(x) \) là:

\[ \int \sin(x) \, dx = -\cos(x) + C \]

Kết quả

\[ \int \sin(x) \, dx = -\cos(x) + C \]

Ví dụ 3: Tích phân từng phần

Tính tích phân của \( x e^x \)

Bước 1: Xác định \( u \) và \( dv \)

Chọn \( u = x \) và \( dv = e^x dx \)

Bước 2: Tính \( du \) và \( v \)

\[ du = dx \]

\[ v = \int e^x dx = e^x \]

Bước 3: Áp dụng công thức tích phân từng phần

\[ \int u \, dv = uv – \int v \, du \]

\[ \int x e^x \, dx = x e^x – \int e^x \, dx \]

\[ = x e^x – e^x + C \]

\[ = e^x (x – 1) + C \]

Kết quả

\[ \int x e^x \, dx = e^x (x – 1) + C \]

Các ví dụ trên minh họa cách sử dụng các công thức tích phân khác nhau để giải các bài toán cụ thể.

Điều này mang lại những hiểu biết sâu sắc về tích phân và giải quyết nhiều vấn đề phức tạp trong thực tế.Cảm ơn bạn đã theo dõi và hỏi về tích phân Riemann. Nếu bạn có thêm câu hỏi hoặc cần sự giúp đỡ về bất kỳ chủ đề nào, đừng ngần ngại liên hệ với tôi. Chúc bạn một ngày tốt lành! Hãy theo dõi trang web thaoluan.edu.vn để có nhiều kiến thức hơn nhé!