Định nghĩa xác suất là gì? Đặc điểm và ứng dụng của xác suất
Trong cuộc sống hàng ngày cũng như trong các lĩnh vực khoa học và kỹ thuật, chúng ta thường phải đối mặt với những tình huống không chắc chắn. Từ việc dự đoán thời tiết, xác định kết quả của một trò chơi may rủi, cho đến phân tích rủi ro trong đầu tư tài chính, khái niệm xác suất đóng một vai trò quan trọng và không thể thiếu.
Xác suất là một nhánh của toán học nghiên cứu về khả năng xảy ra của các sự kiện. Nó giúp chúng ta định lượng và phân tích mức độ không chắc chắn, từ đó đưa ra các quyết định sáng suốt hơn. Trong bài viết này, chúng ta sẽ tìm hiểu chi tiết về định nghĩa xác suất, các đặc điểm cơ bản của nó, và những ứng dụng quan trọng trong cuộc sống và khoa học.
Định nghĩa xác suất

Xác suất là một khái niệm trong toán học dùng để đo lường khả năng xảy ra của một sự kiện nào đó. Nó được biểu diễn bằng một số từ 0 đến 1, trong đó 0 biểu thị sự kiện không thể xảy ra và 1 biểu thị sự kiện chắc chắn xảy ra.
Cụ thể hơn, xác suất của một sự kiện \( A \) được định nghĩa là tỷ lệ giữa số lượng kết quả thuận lợi cho sự kiện \( A \) và tổng số lượng kết quả có thể xảy ra trong không gian mẫu. Công thức xác suất của sự kiện \( A \) được viết như sau:
\[ P(A) = \frac{\text{Số kết quả thuận lợi cho sự kiện } A}{\text{Tổng số kết quả có thể xảy ra trong không gian mẫu}} \]
Ví dụ, khi tung một con xúc xắc, xác suất để ra mặt số 3 là:
\[ P(\text{ra số 3}) = \frac{1}{6} \]
vì có 1 kết quả thuận lợi (mặt số 3) trong tổng số 6 kết quả có thể xảy ra (các mặt số 1, 2, 3, 4, 5, 6).
Xác suất giúp chúng ta hiểu và dự đoán các sự kiện ngẫu nhiên, từ đó áp dụng vào nhiều lĩnh vực khác nhau như khoa học, kinh tế, và đời sống hàng ngày.
Các cách tính xác suất
Có nhiều phương pháp để tính xác suất của một sự kiện. Dưới đây là các cách phổ biến:
Xác suất cổ điển (Classical Probability)
Phương pháp này áp dụng cho các tình huống mà tất cả các kết quả có thể xảy ra đều có khả năng như nhau. Xác suất của một sự kiện \(A\) được tính bằng công thức:
\[ P(A) = \frac{\text{Số kết quả thuận lợi cho sự kiện } A}{\text{Tổng số kết quả có thể xảy ra trong không gian mẫu}} \]
Ví dụ: Khi tung một đồng xu, xác suất để ra mặt ngửa là:
\[ P(\text{ngửa}) = \frac{1}{2} \]
Xác suất thực nghiệm (Empirical Probability)
Phương pháp này dựa trên việc thực hiện thí nghiệm hoặc quan sát nhiều lần và tính xác suất dựa trên kết quả thực tế thu được. Xác suất thực nghiệm của một sự kiện \(A\) được tính bằng:
\[ P(A) = \frac{\text{Số lần sự kiện } A \text{ xảy ra}}{\text{Tổng số lần thí nghiệm hoặc quan sát}} \]
Ví dụ: Nếu tung một đồng xu 100 lần và có 55 lần ra mặt ngửa, xác suất thực nghiệm để ra mặt ngửa là:
\[ P(\text{ngửa}) = \frac{55}{100} = 0.55 \]
Xác suất định nghĩa thông qua tần suất tương đối (Relative Frequency)
Phương pháp này sử dụng các dữ liệu lịch sử hoặc tần suất tương đối của các sự kiện để tính xác suất. Nó cũng được tính bằng:
\[ P(A) = \frac{\text{Số lần sự kiện } A \text{ xảy ra}}{\text{Tổng số lần thí nghiệm hoặc quan sát}} \]
Xác suất có điều kiện (Conditional Probability)
Xác suất có điều kiện là xác suất của một sự kiện xảy ra khi biết rằng một sự kiện khác đã xảy ra. Xác suất có điều kiện của sự kiện \(A\) khi biết sự kiện \(B\) đã xảy ra được tính bằng:
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
trong đó \( P(A \cap B) \) là xác suất của cả hai sự kiện \( A \) và \( B \) xảy ra.
Ví dụ: Trong một túi có 3 quả táo và 2 quả cam, xác suất để lấy được một quả cam sau khi đã lấy một quả táo ra ngoài là:
\[ P(\text{cam | đã lấy táo}) = \frac{2}{4} = 0.5 \]
Xác suất Bayes (Bayesian Probability)

Phương pháp này sử dụng định lý Bayes để tính xác suất của một sự kiện dựa trên thông tin có trước và thông tin mới. Công thức Bayes:
\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]
Ví dụ: Trong một bài toán y học, xác suất để một người có bệnh khi biết kết quả xét nghiệm dương tính có thể được tính bằng định lý Bayes.
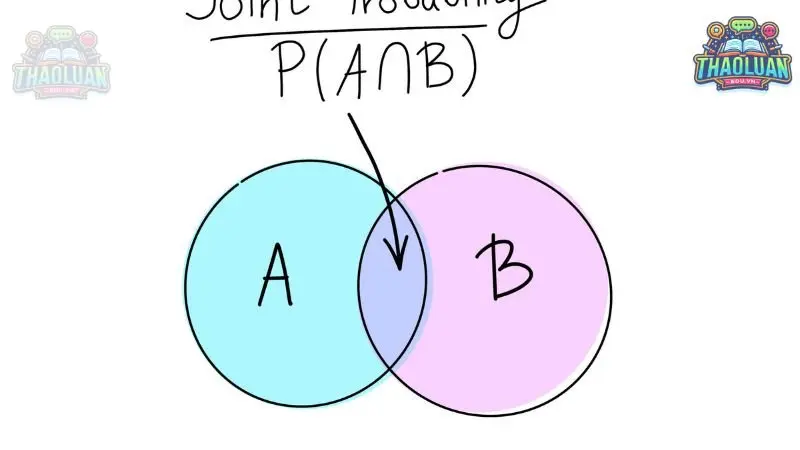
Xác suất kết hợp (Joint Probability)
Xác suất kết hợp là xác suất của việc hai hoặc nhiều sự kiện xảy ra đồng thời. Đối với các sự kiện độc lập, xác suất kết hợp của hai sự kiện \( A \) và \( B \) là:
\[ P(A \cap B) = P(A) \cdot P(B) \]
Ví dụ: Xác suất để ra mặt ngửa khi tung hai đồng xu là:
\[ P(\text{ngửa và ngửa}) = P(\text{ngửa}) \cdot P(\text{ngửa}) = \frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4} \]
Các phương pháp trên giúp chúng ta tính xác suất trong nhiều tình huống khác nhau, từ những tình huống đơn giản với các kết quả đồng đều, đến những tình huống phức tạp yêu cầu thông tin từ dữ liệu thực nghiệm hoặc điều kiện bổ sung. Việc hiểu và áp dụng đúng phương pháp tính xác suất là rất quan trọng trong việc giải quyết các bài toán xác suất trong thực tế.
Đặc điểm của xác suất
Xác suất là một khái niệm quan trọng trong toán học và thống kê, có nhiều đặc điểm quan trọng giúp định hình cách chúng ta hiểu và làm việc với nó. Dưới đây là các đặc điểm chính của xác suất
Giá trị trong khoảng [0, 1]
Xác suất của bất kỳ sự kiện nào luôn nằm trong khoảng từ 0 đến 1.
Xác suất bằng 0 nghĩa là sự kiện không thể xảy ra.
Xác suất bằng 1 nghĩa là sự kiện chắc chắn xảy ra.
Tổng xác suất của không gian mẫu bằng 1
Tổng xác suất của tất cả các kết quả có thể xảy ra trong một không gian mẫu bằng 1.
Nếu \(S\) là không gian mẫu, thì \( P(S) = 1 \).
Xác suất của các sự kiện phụ thuộc và độc lập
Đối với các sự kiện độc lập \(A\) và \(B\), xác suất của cả hai sự kiện xảy ra bằng tích xác suất của từng sự kiện
\[ P(A \cap B) = P(A) \cdot P(B) \]
Đối với các sự kiện phụ thuộc, xác suất của cả hai sự kiện xảy ra phải tính theo xác suất có điều kiện
\[ P(A \cap B) = P(A) \cdot P(B|A) \]
Xác suất của sự kiện đối lập (bù)
Xác suất của sự kiện đối lập (bù) của một sự kiện \(A\) là:
\[ P(A’) = 1 – P(A) \]
Sự kiện đối lập \(A’\) là sự kiện mà \(A\) không xảy ra.
Nguyên lý cộng xác suất (nguyên tắc bao phủ)
Đối với các sự kiện rời rạc (không giao nhau) \(A\) và \(B\), xác suất của một trong hai sự kiện xảy ra là
\[ P(A \cup B) = P(A) + P(B) \]
Đối với các sự kiện có giao nhau
\[ P(A \cup B) = P(A) + P(B) – P(A \cap B) \]
Tính cộng và tính nhân
Xác suất tuân theo các tính chất cộng và nhân:
Tính cộng áp dụng cho các sự kiện không giao nhau.
Tính nhân áp dụng cho các sự kiện độc lập.
Định lý Bayes
Định lý Bayes cung cấp một cách để tính xác suất của một sự kiện dựa trên thông tin có trước và bằng chứng mới
\[ P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} \]
Đây là công cụ quan trọng trong nhiều lĩnh vực như y học, tài chính và học máy.
Xác suất có điều kiện
Xác suất của một sự kiện \(A\) khi biết rằng sự kiện \(B\) đã xảy ra được gọi là xác suất có điều kiện và được tính bằng
\[ P(A|B) = \frac{P(A \cap B)}{P(B)} \]
Những đặc điểm của xác suất giúp chúng ta hiểu rõ hơn về cách tính toán và áp dụng xác suất trong các tình huống khác nhau. Từ việc dự đoán các sự kiện đơn giản đến phân tích các hệ thống phức tạp, hiểu rõ các đặc điểm này là nền tảng cho việc sử dụng xác suất một cách hiệu quả trong đời sống và nghiên cứu khoa học.

Biến cố ngẫu nhiên của xác suất
Biến cố ngẫu nhiên là một khái niệm cơ bản trong lý thuyết xác suất, dùng để mô tả một tập hợp con của không gian mẫu. Biến cố ngẫu nhiên là một sự kiện có thể xảy ra hoặc không xảy ra khi một thí nghiệm ngẫu nhiên được thực hiện. Dưới đây là các khái niệm cơ bản liên quan đến biến cố ngẫu nhiên.
Khái niệm biến cố ngẫu nhiên
Biến cố ngẫu nhiên (event) là một tập hợp con của không gian mẫu \(S\). Nếu \(A\) là một biến cố, thì \(A \subseteq S\).
Không gian mẫu (sample space) là tập hợp tất cả các kết quả có thể xảy ra của một thí nghiệm ngẫu nhiên. Ký hiệu là \(S\).
Phân loại biến cố ngẫu nhiên
Biến cố chắc chắn (certain event) là biến cố mà chắc chắn xảy ra. Nó chính là không gian mẫu \(S\). \(P(S) = 1\).
Biến cố không thể (impossible event) là biến cố không bao giờ xảy ra. Nó là tập rỗng \(\emptyset\). \(P(\emptyset) = 0\).
Biến cố đơn (simple event) là biến cố chỉ gồm một kết quả duy nhất.
Biến cố phức hợp (compound event) là biến cố gồm nhiều kết quả.
Các phép toán trên biến cố ngẫu nhiên
Phép hợp (union): Biến cố \(A \cup B\) xảy ra khi ít nhất một trong hai biến cố \(A\) hoặc \(B\) xảy ra.
\[ P(A \cup B) = P(A) + P(B) – P(A \cap B) \]
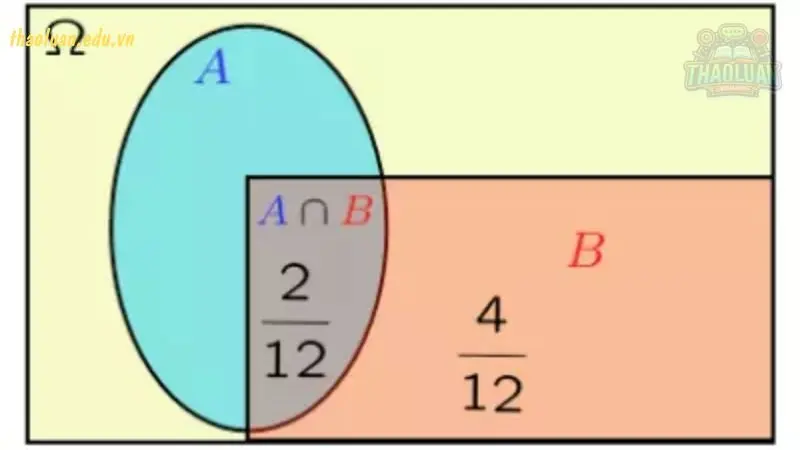
Phép giao (intersection): Biến cố \(A \cap B\) xảy ra khi cả hai biến cố \(A\) và \(B\) cùng xảy ra.
\[ P(A \cap B) = P(A) \cdot P(B|A) \] nếu \(A\) và \(B\) là các biến cố phụ thuộc.
\[ P(A \cap B) = P(A) \cdot P(B) \] nếu \(A\) và \(B\) là các biến cố độc lập.
Phép bù (complement): Biến cố \(A’\) (hoặc \( \bar{A} \)) xảy ra khi biến cố \(A\) không xảy ra.
\[ P(A’) = 1 – P(A) \]
Xác suất của biến cố ngẫu nhiên
Xác suất của một biến cố ngẫu nhiên là một số đo mức độ chắc chắn của biến cố đó, và được tính toán theo quy tắc xác suất
Xác suất của biến cố hợp
\[ P(A \cup B) = P(A) + P(B) – P(A \cap B) \]
Xác suất của biến cố bù
\[ P(A’) = 1 – P(A) \]
Xác suất của biến cố giao (nếu \(A\) và \(B\) là độc lập)
\[ P(A \cap B) = P(A) \cdot P(B) \]
Ví dụ về biến cố ngẫu nhiên
Ví dụ 1: Khi tung một con xúc xắc, không gian mẫu \(S\) là \(\{1, 2, 3, 4, 5, 6\}\). Biến cố \(A\) là ra số chẵn, vậy \(A = \{2, 4, 6\}\).
Ví dụ 2: Khi rút một lá bài từ bộ bài 52 lá, không gian mẫu \(S\) là tất cả các lá bài. Biến cố \(B\) là rút được lá bài cơ, vậy \(B\) gồm 13 lá bài cơ.
Tính chất của biến cố ngẫu nhiên
Luật cộng xác suất: Nếu hai biến cố không thể xảy ra đồng thời (rời rạc), xác suất của biến cố hợp bằng tổng xác suất của từng biến cố.
\[ P(A \cup B) = P(A) + P(B) \]
Luật giao xác suất: Nếu hai biến cố độc lập, xác suất của biến cố giao bằng tích xác suất của từng biến cố.
\[ P(A \cap B) = P(A) \cdot P(B) \]
Biến cố ngẫu nhiên là một phần quan trọng trong lý thuyết xác suất, giúp chúng ta hiểu và phân tích các hiện tượng ngẫu nhiên. Việc nắm vững các khái niệm và phép toán liên quan đến biến cố ngẫu nhiên là cơ sở để giải quyết các bài toán xác suất trong thực tế.
Ứng dụng của xác suất
Xác suất có vai trò quan trọng và được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau của đời sống và khoa học. Dưới đây là một số ứng dụng tiêu biểu của xác suất:
Khoa học và kỹ thuật
Vật lý và hóa học: Xác suất được sử dụng để mô tả các hiện tượng ngẫu nhiên ở mức độ phân tử, như sự phân bố các hạt trong một hệ thống, phản ứng hóa học, và động học chất khí.
Kỹ thuật: Trong kỹ thuật, xác suất giúp phân tích và dự đoán độ tin cậy của các hệ thống, chẳng hạn như hệ thống điện, cơ khí, và máy tính. Điều này giúp đảm bảo rằng các hệ thống hoạt động đúng như mong đợi và có độ bền cao.
Kinh tế và tài chính
Phân tích rủi ro: Xác suất được sử dụng để đánh giá và quản lý rủi ro trong đầu tư, bảo hiểm, và các hoạt động tài chính khác. Ví dụ, mô hình VAR (Value at Risk) được sử dụng để ước tính mức lỗ tối đa có thể xảy ra trong một khoảng thời gian nhất định với một mức độ tin cậy nhất định.
Dự báo kinh tế: Các mô hình xác suất được sử dụng để dự báo các chỉ số kinh tế như GDP, lạm phát, và tỷ lệ thất nghiệp. Điều này giúp các nhà hoạch định chính sách và doanh nghiệp đưa ra các quyết định chiến lược.
Y học và sinh học
Chẩn đoán và điều trị: Xác suất giúp xác định xác suất mắc bệnh dựa trên các triệu chứng và kết quả xét nghiệm. Phương pháp này giúp các bác sĩ chẩn đoán chính xác hơn và lựa chọn phương pháp điều trị hiệu quả.
Nghiên cứu lâm sàng: Trong nghiên cứu lâm sàng, xác suất được sử dụng để thiết kế và phân tích các thử nghiệm lâm sàng, giúp xác định hiệu quả và an toàn của các phương pháp điều trị mới.
Thống kê và dữ liệu
Phân tích dữ liệu: Xác suất là nền tảng của thống kê, giúp phân tích dữ liệu và rút ra kết luận từ các mẫu dữ liệu. Các kỹ thuật thống kê dựa trên xác suất như kiểm định giả thuyết, ước lượng khoảng, và phân tích hồi quy được sử dụng rộng rãi trong nhiều lĩnh vực.
Khoa học dữ liệu và học máy: Các mô hình xác suất được sử dụng trong khoa học dữ liệu và học máy để dự đoán kết quả, phân loại dữ liệu, và phát hiện các mẫu ẩn trong dữ liệu lớn.
Thời tiết và khí hậu
Dự báo thời tiết: Các mô hình xác suất được sử dụng để dự báo thời tiết và biến đổi khí hậu. Điều này giúp các nhà khí tượng học dự báo chính xác hơn về nhiệt độ, lượng mưa, và các hiện tượng thời tiết khác.
Đánh giá rủi ro thiên tai: Xác suất giúp đánh giá rủi ro và tần suất xảy ra của các hiện tượng thiên tai như động đất, bão, và lũ lụt, từ đó giúp các cơ quan chức năng chuẩn bị và ứng phó hiệu quả.
Trò chơi và cờ bạc
Thiết kế trò chơi: Xác suất được sử dụng để thiết kế các trò chơi công bằng và cân bằng, chẳng hạn như trò chơi điện tử và các trò chơi bài.
Quản lý sòng bạc: Trong ngành công nghiệp cờ bạc, xác suất giúp quản lý và tối ưu hóa lợi nhuận, đồng thời đảm bảo tính công bằng cho người chơi.
Xã hội và hành vi con người
Khoa học xã hội: Xác suất được sử dụng để phân tích hành vi con người và xã hội, chẳng hạn như các cuộc khảo sát ý kiến công chúng, nghiên cứu thị trường, và phân tích dữ liệu dân số.
Tâm lý học: Trong tâm lý học, xác suất giúp nghiên cứu các hiện tượng tâm lý và hành vi, từ đó phát triển các lý thuyết và phương pháp điều trị tâm lý hiệu quả.
Xác suất là một công cụ mạnh mẽ và linh hoạt, có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Từ khoa học tự nhiên đến xã hội, từ kinh tế đến y học, hiểu biết và sử dụng xác suất một cách hiệu quả giúp chúng ta đưa ra các quyết định chính xác và sáng suốt hơn, đồng thời góp phần cải thiện chất lượng cuộc sống. Hy vọng rằng các kiến thức về xác suất sẽ được áp dụng rộng rãi và mang lại nhiều lợi ích thiết thực trong cuộc sống hàng ngày. Cảm ơn bạn đã theo dõi trang thaoluan.edu.vn!

Bài tập vận dụng xác Suất
Dưới đây là một số bài tập vận dụng lý thuyết xác suất để giúp bạn hiểu rõ hơn về cách áp dụng các nguyên tắc và công thức vào các tình huống thực tế.
Bài tập 1: Tung xúc xắc
Đề bài: Một con xúc xắc chuẩn có 6 mặt, đánh số từ 1 đến 6. Tung một con xúc xắc. Tính xác suất của các biến cố sau
- Số chấm xuất hiện là số chẵn.
- Số chấm xuất hiện là số nguyên tố.
- Số chấm xuất hiện là lớn hơn 4.
Lời giải
Số chẵn: Các số chẵn trên con xúc xắc là 2, 4, 6. Tổng số kết quả có thể là 6. Do đó, xác suất là
\[P(\text{số chẵn}) = \frac{3}{6} = \frac{1}{2}\]
Số nguyên tố: Các số nguyên tố trên con xúc xắc là 2, 3, 5. Do đó, xác suất là
\[P(\text{số nguyên tố}) = \frac{3}{6} = \frac{1}{2}\]
Lớn hơn 4: Các số lớn hơn 4 là 5, 6. Do đó, xác suất là
\[P(\text{lớn hơn 4}) = \frac{2}{6} = \frac{1}{3}\]
Bài tập 2: Rút thẻ bài
Đề bài: Một bộ bài chuẩn có 52 lá. Tính xác suất để rút được
- Một lá bài cơ.
- Một lá bài hình (J, Q, K).
- Một lá bài là quân át (A).
Lời giải
Lá bài cơ: Có 13 lá bài cơ trong bộ bài 52 lá. Do đó, xác suất là
\[P(\text{lá bài cơ}) = \frac{13}{52} = \frac{1}{4}\]
Lá bài hình: Có 12 lá bài hình (J, Q, K của mỗi loại: cơ, rô, chuồn, bích). Do đó, xác suất là:
\[P(\text{lá bài hình}) = \frac{12}{52} = \frac{3}{13}\]
Lá bài át: Có 4 quân át (mỗi loại một quân). Do đó, xác suất là:
\[P(\text{quân át}) = \frac{4}{52} = \frac{1}{13}\]
Bài tập 3: Đèn giao thông
Đề bài: Ở một ngã tư, đèn giao thông chuyển đổi giữa 3 trạng thái: xanh, vàng, đỏ. Giả sử xác suất cho mỗi trạng thái là như nhau. Tính xác suất để
- Đèn đang ở trạng thái xanh.
- Đèn không ở trạng thái vàng.
Lời giải
Trạng thái xanh: Vì có 3 trạng thái và mỗi trạng thái có xác suất bằng nhau, xác suất đèn ở trạng thái xanh là
\[P(\text{trạng thái xanh}) = \frac{1}{3}\]
Không ở trạng thái vàng: Xác suất để đèn không ở trạng thái vàng là tổng xác suất của hai trạng thái còn lại (xanh và đỏ)
\[P(\text{không ở trạng thái vàng}) = 1 – P(\text{trạng thái vàng}) = 1 – \frac{1}{3} = \frac{2}{3}\]
Bài tập 4: Bóng đá
Đề bài: Một đội bóng đá có 3 trận đấu. Xác suất để đội thắng một trận là 0.5. Tính xác suất để đội bóng này
- Thắng ít nhất một trận.
- Thắng đúng hai trận.
Lời giải
Thắng ít nhất một trận
Xác suất thua cả ba trận là
\[P(\text{thua cả ba trận}) = (0.5)^3 = 0.125\]
Xác suất thắng ít nhất một trận là:
\[P(\text{thắng ít nhất một trận}) = 1 – P(\text{thua cả ba trận}) = 1 – 0.125 = 0.875\]
Những bài tập trên giúp bạn áp dụng các nguyên tắc xác suất để giải quyết các tình huống cụ thể. Hiểu và thực hành các bài toán xác suất sẽ giúp bạn nắm vững lý thuyết và có khả năng áp dụng vào nhiều lĩnh vực khác nhau trong thực tế.

Xác suất là một lĩnh vực quan trọng và thú vị trong toán học, với nhiều ứng dụng rộng rãi trong cuộc sống hàng ngày và các ngành khoa học. Từ việc dự đoán thời tiết, đánh giá rủi ro tài chính, đến phân tích dữ liệu trong y học và kỹ thuật, xác suất cung cấp các công cụ mạnh mẽ để hiểu và dự đoán các hiện tượng ngẫu nhiên.
Hy vọng rằng qua các bài tập vận dụng và các ví dụ cụ thể, bạn đã có cái nhìn sâu sắc hơn về xác suất và cách áp dụng nó vào thực tế. Việc nắm vững các khái niệm và công thức xác suất không chỉ giúp bạn trong học tập mà còn mang lại nhiều lợi ích thiết thực trong công việc và cuộc sống.Hãy theo dõi thaoluan.edu.com!